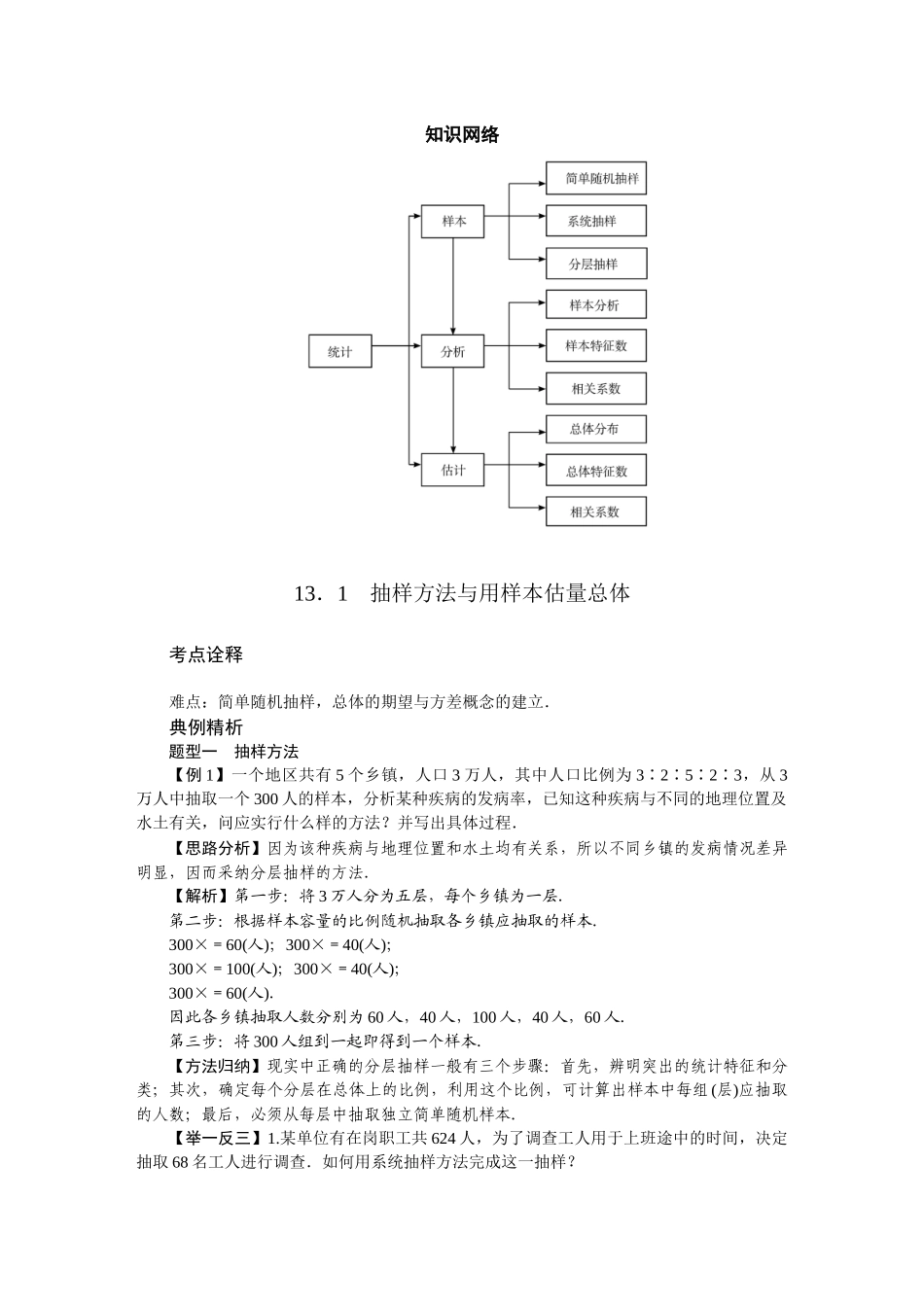
第十三章 统计案例高考导航考纲要求备考策略 1.理解随机抽样的必要性和重要性,会用简单随机抽样方法从总体中抽取样本,了解分层抽样和系统抽样方法. 2.了解分布的意义和作用,会列频率分布表,会画频率分布直方图、茎叶图,理解它们各自的特点,理解样本数据标准差的意义和作用,会计算数据标准差,能从样本数据中提取基本的数字特征(如平均数、标准差),并作出合理的解释,会用样本的频率分布估量总体分布,会用样本的基本数字特征估量总体的基本数字特征,理解用样本估量总体的思想,会用随机抽样的基本方法和样本估量总体的思想解决一些简单的实际问题. 3.会作两个有关联变量的散点图,会利用散点图认识变量间的相关关系,了解最小二乘法的思想,能根据给出的线性回归方程系数公式建立线性回归方程,了解回归的基本思想、方法及其简单应用. 4.了解独立性检验(只要求 2×2 列联表)的基本思想、方法及其简单应用.统计案例是高中数学中应用性的章节,也是高考必考内容,湖南省 2024 年高考对本章内容考查的是第 4 题,5 分,多数以选择、填空题形式考查,考点往往集中体现在抽样方法、频率分布图表方面,近几年对回归分析与独立性检验也有考查,应引起重视.复习时采纳以下应对策略: 1.立足课本,突出基础,重视概念的辨析与理解. 2.注重“操作”训练,如抽样方法的操作步骤,频率分布表和频率分布直方图、茎叶图的绘制等,要熟练掌握. 3.重视统计与概率的综合运用,会用样本频率分布估量总体分布,会用样本平均数估量总体期望值,会用样本的方差估量总体方差;提高搜集处理信息及分析解决问题的能力. 4.加强统计应用性的训练,能用统计的方法提供决策、制定方案.知识网络13.1 抽样方法与用样本估量总体考点诠释难点:简单随机抽样,总体的期望与方差概念的建立.典例精析题型一 抽样方法【例 1】一个地区共有 5 个乡镇,人口 3 万人,其中人口比例为 3∶2∶5∶2∶3,从 3万人中抽取一个 300 人的样本,分析某种疾病的发病率,已知这种疾病与不同的地理位置及水土有关,问应实行什么样的方法?并写出具体过程.【思路分析】因为该种疾病与地理位置和水土均有关系,所以不同乡镇的发病情况差异明显,因而采纳分层抽样的方法.【解析】第一步:将 3 万人分为五层,每个乡镇为一层.第二步:根据样本容量的比例随机抽取各乡镇应抽取的样本.300×=60(人);300×=40(人);300×=100(人);300×=40(人);300×=60(...