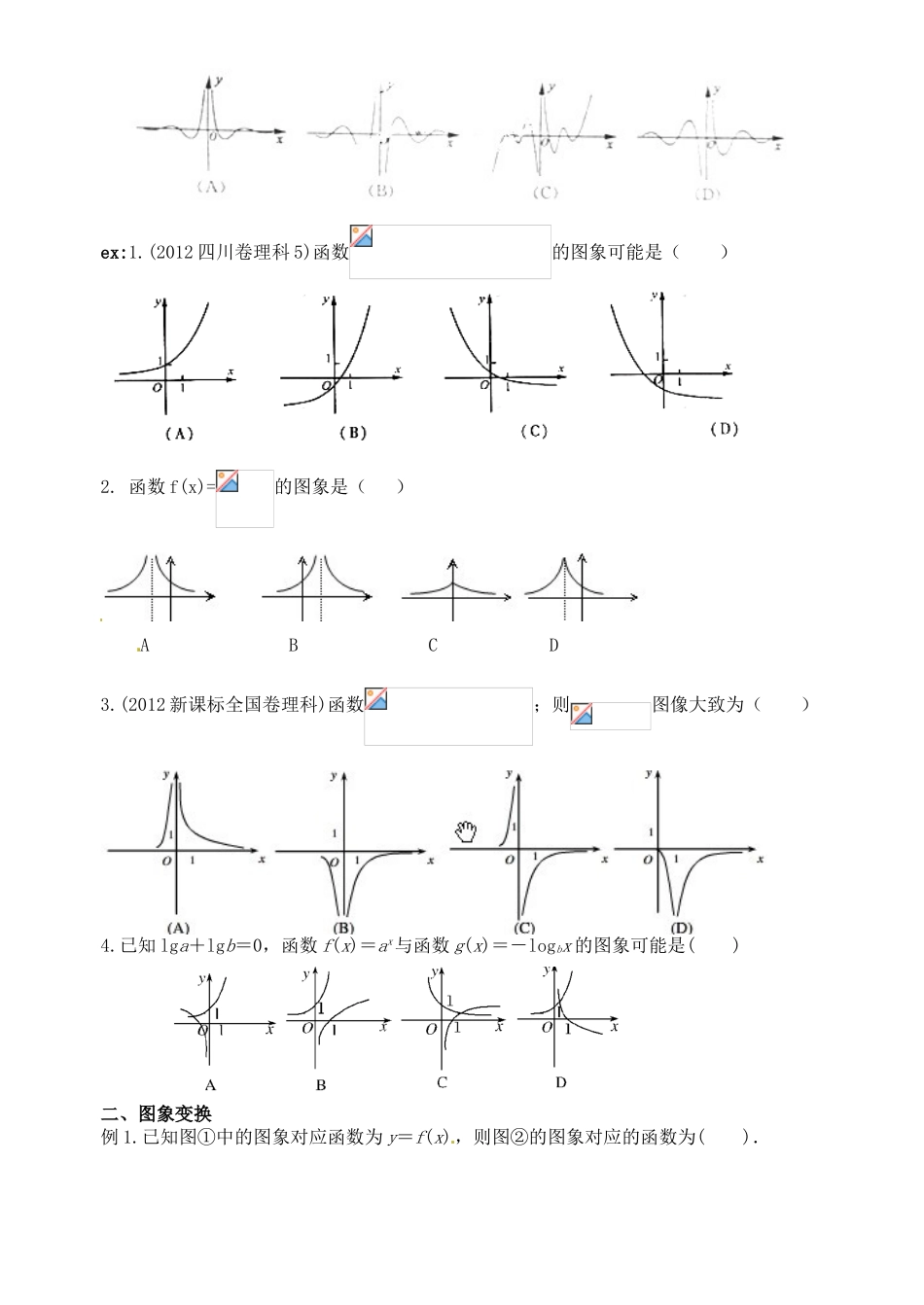
广东省佛山市中大附中三水实验中学高三数学《2.5 函数的图像》基础复习学案 新人教 A 版 [研读考纲][知识梳理][备考建议]函数图象是研究函数性质、方程、不等式的重要工具,是数形结合的基础,是高考考查的热点,复习时,应重点掌握几种基本初等函数的图 象,并在审题、识图上多下功夫,学会分析“数”与“形”的结合点,把几种常见题型的解法技巧理解透彻.[方法提示]一条主线数形结合的思想方法是学习函数内容的一条主线,也是高考考查的热点.作函数图象首先要明确函数图象的形状和位置,而取值、列表、描点、连线只是作函数图象的辅助手段,不可本末倒置.两个区别(1)一个函数的图象关于原点对称与两个函数的图象关于原点对称不同,前者是自身对称,且为奇函数,后者是两个不同的函数对称.(2)一个函数的图象关于 y 轴对称与两个函数的图象关于 y 轴对称也不同,前者也是自身对称,且为偶函数,后者也是两个不同函数的对称关系.三种途径明确函数图象形状和位置的方法大致有以下三种途径.(1)图象变换:平移变换、伸缩变换、对称变换.(2)函数解析式的等价变换.(3)研究函数的性质.[考向训练]一、知式选图、知图选式例 1. 给出四个函数,分别满足① f(x+y)=f(x)+f(y),② g(x+y)=g(x)·g(y),③ h(x·y)=h(x)+h(y),④ m(x·y)=m(x)·m(y).又给出四个函数的图象,那么正确的匹配方案可以是( )A.①甲,②乙,③丙,④丁 B. ① 乙,②丙,③甲,④丁C. ① 丙,②甲,③乙,④丁 D. ① 丁,②甲,③乙,④丙2.(2012 山东卷理科 9)函数的图像大致为( )ex:1.(2012 四川卷理科 5)函数的图象可能是( )2. 函数 f(x)=的图象是( )A B C D3.(2012 新课标全国卷理科)函数;则图像大致为( )4.已知 lga+lgb=0,函数 f(x)=ax与函数 g(x)=-logbx 的图象可能是( )二、图象变换例 1.已知图①中的图象对应函数为 y=f(x),则图②的图象对应的函数为( ).A.y=f(|x|) B.y=|f(x)| C.y=f(-|x|) D.y=-f(|x|)2.(2011 陕西理 3)设函数(R)满足,,则函数的图像是 ( )ex:1. 函数 y=f(x)的图象如图所示,则函数 y=-f(x+1)的图象大致为 ( ) A B C D2. 函数 y=f(x)的曲线 如左图所示,那么函数 y=f(2-x)的曲线是( )3.已知函数 f(x)定义在[-2,2]上的图象如图所示,请分别画出下列函数的图象:(1)y=f(x+1) (2)y=f(x)+1; (3)y=f(-x); (4)y=-f(x)...