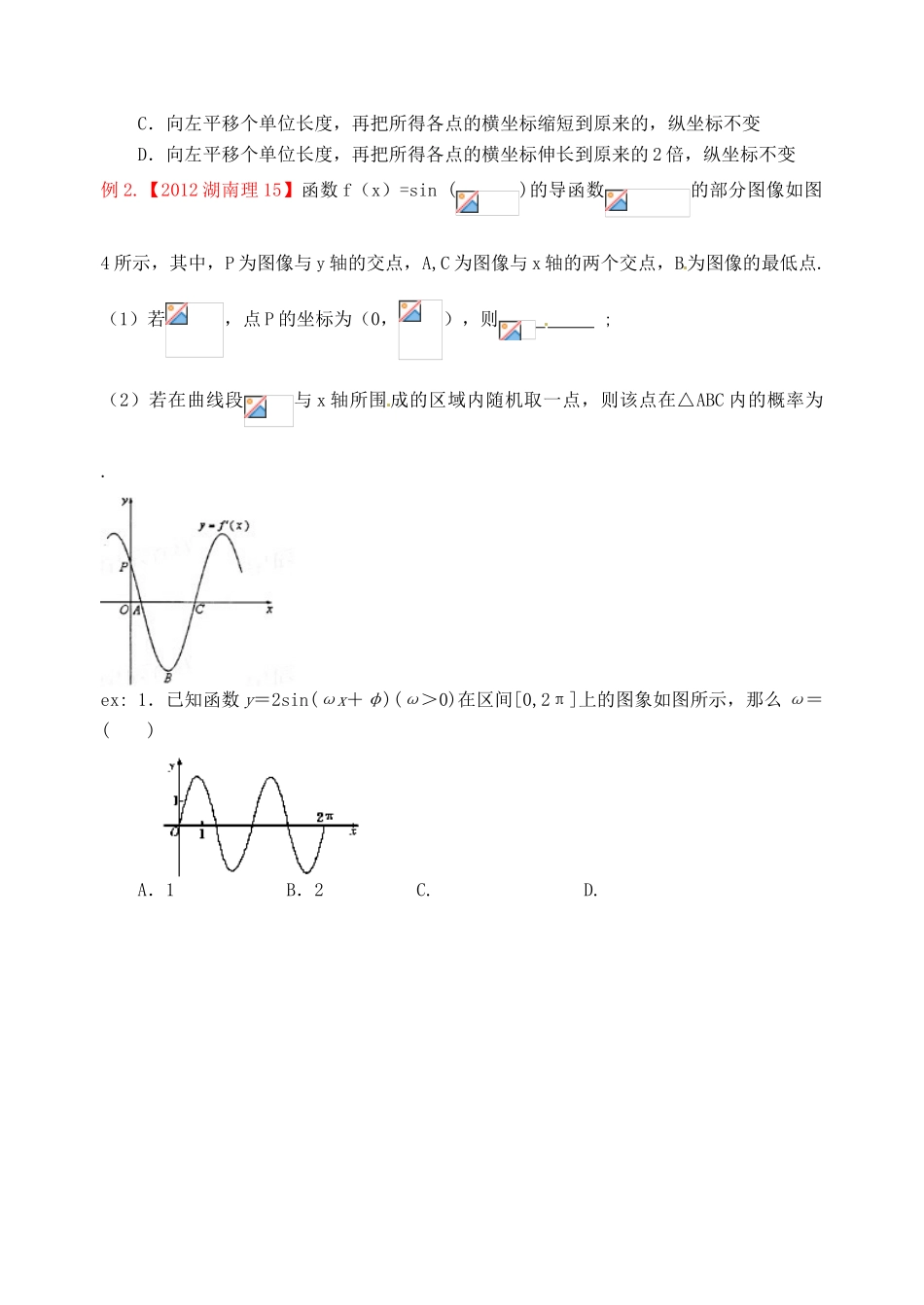
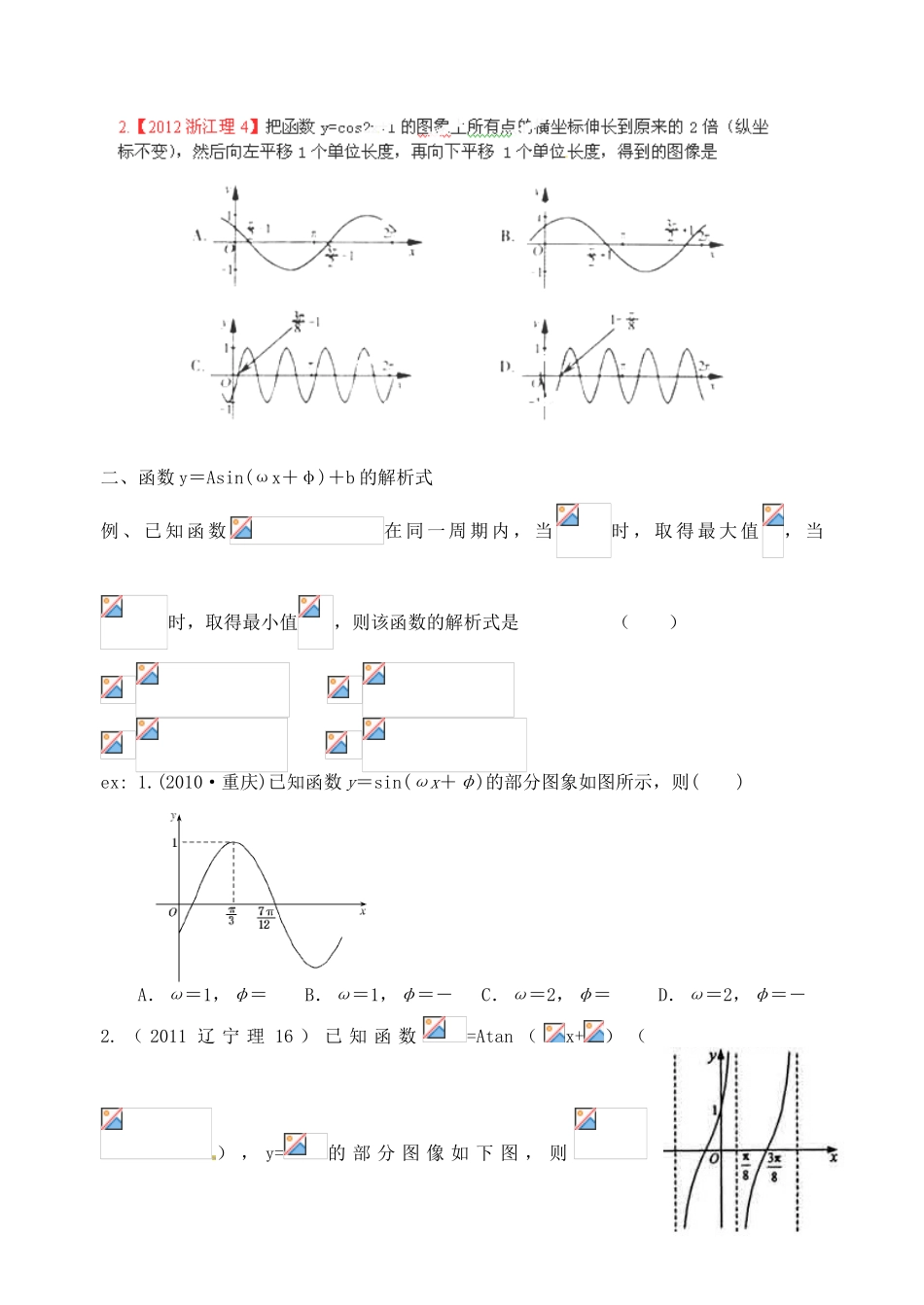
广东省佛山市中大附中三水实验中学高三数学《3.6 函数 y=Asin((ωx+φ)的图象及三角函数模型的简单应用》基础复习学案 新人教 A 版 [研读考纲][知识梳理][备考建议]本讲复习时,重点掌握正弦型函数 y=Asin(ωx+φ)的图象的“五点”作图法,图象的三种变换方法,以及利用三角函数的性质解决有关问题. [方法提示]一种方法在由图象求三角函数解析式时,若最大值为 M,最小值为 m,则 A=,k=,ω 由周期 T 确定,即由=T 求出,φ 由特殊点确定.一个区别由 y=sin x 的图象变换到 y=Asin (ωx+φ)的图象,两种变换的区别:先相位变换再周期变换(伸缩变换),平移的量是|φ|个单位;而先周期变换(伸缩变换)再相位变换,平移的量是(ω>0)个单位.原因在于相位变换和周期变换都是针对 x 而言,即 x 本身加减多少值,而不是依赖于 ωx 加减多少值. 两个注意作正弦型函数 y=Asin(ωx+φ)的图象时应注意:(1)首先要确定函数的定义域;(2)对于具有周期性的函数,应先 求出周期,作图象时只要作出一个周期的图象,就可根据周期性作出整个函数的图象.[考向训练]一、三角函数图象及变换A.向左平移个单位长度,再把所得各点的横坐标缩短到原来的,纵坐标不变B.向左平移个单位长度,再把所得各点的横坐标伸长到原来的 2 倍,纵坐标不变C.向左平移个单位长度,再把所得各点的横坐标缩短到原来的,纵坐标不变D.向左平移个单位长度,再把所得各点的横坐标伸长到原来的 2 倍,纵坐标不变例 2.【2012 湖南理 15】函数 f(x)=sin ()的导函数的部分图像如图4 所示,其中,P 为图像与 y 轴的交点,A,C 为图像与 x 轴的两个交点,B为图像的最低点.(1)若,点 P 的坐标为(0,),则 ;(2)若在曲线段与 x 轴所围 成的区域内随机取一点,则该点在△ABC 内的概率为 .ex: 1.已知函数 y=2sin(ωx+φ)(ω>0)在区间[0,2π]上的图象如图所示,那么 ω=( )A.1 B.2 C. D.二、函数 y=Asin(ωx+φ)+b 的解析式例 、 已 知 函 数在 同 一 周 期 内 , 当时 , 取 得 最 大 值, 当时,取得最小值,则该函数的解析式是 ( ) ex: 1.(2010·重庆)已知函数 y=sin(ωx+φ)的部分图象如图所示,则( )A.ω=1,φ= B.ω=1,φ=- C.ω=2,φ= D.ω=2,φ=-2. ( 2011 辽 宁 理 16 ) 已 知 函 数=Atan (x+) () , y=的 部 分 ...