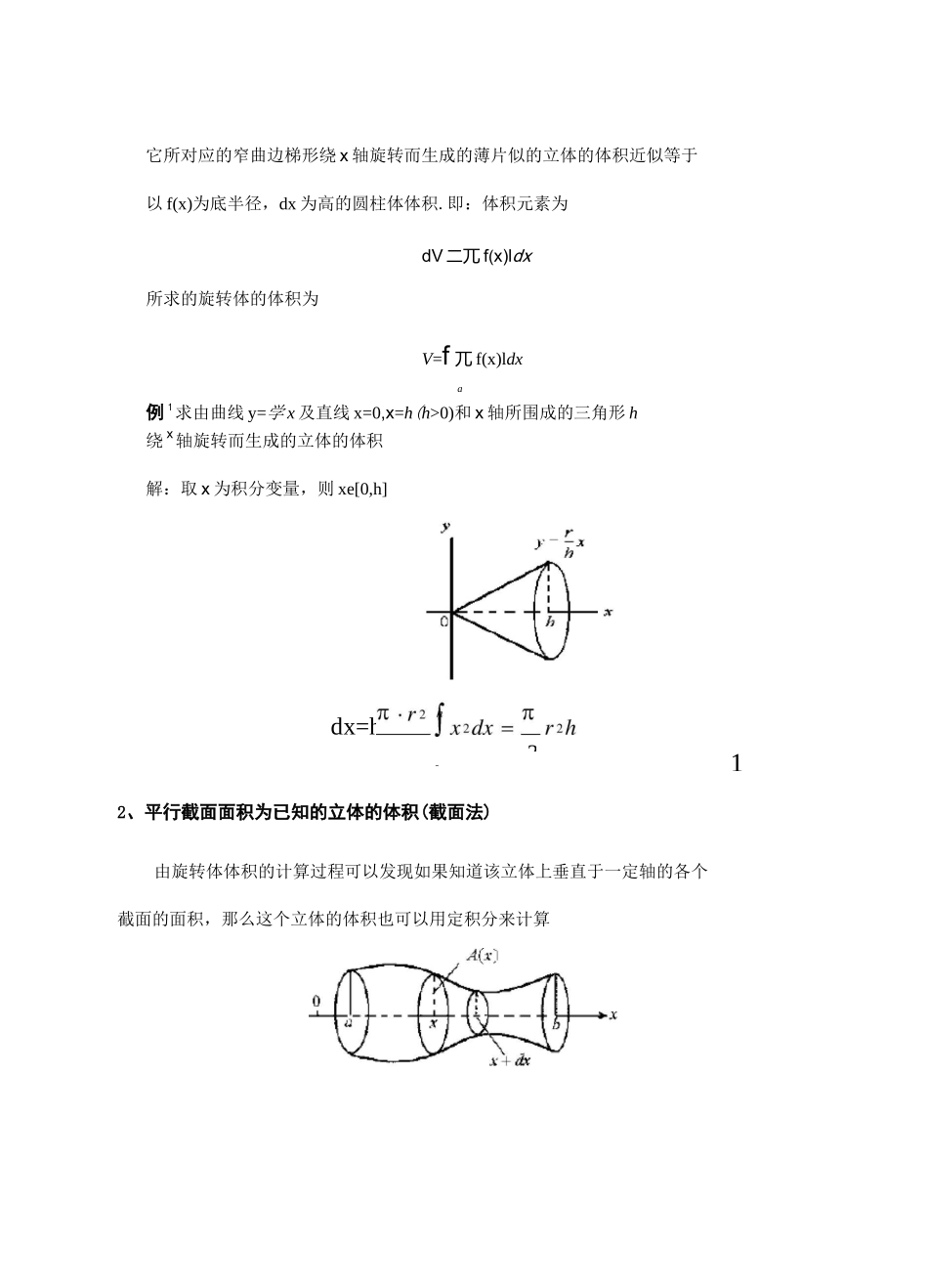
授课课题定积分的应用(_)教学目标和要求掌握利用定积分来求解平面图形的面积和旋转体的体积教学重点和难点平面图形的面积旋转体的体积教学方法情景教学法教学手段板书 PPT授课时间第 18 周课时累计53-54教学过程教学步骤及教学内容时间分配5―,复习引入(1)前面学习了定积分的求解方法也与原函数有关(2)并且掌握了定积分的直接积分法(3)学会了定积分的换元积分法与分布积分法(4)那么我们定积分在实际应用中主要起到什么样的作用呢?新课:二体积1、旋转体的体积旋转体是由一个平面图形绕该平面内一条定直线旋转一周而生成的立体,该定直线称为旋转轴.计算由曲线y=f(x)直线 x=a,x=b及x 轴所围成的曲边梯形,绕 x轴旋转一周而生成的立体的体积.dx=h21它所对应的窄曲边梯形绕 x 轴旋转而生成的薄片似的立体的体积近似等于以 f(x)为底半径,dx 为高的圆柱体体积.即:体积元素为dV 二兀 f(x)ldx所求的旋转体的体积为V=f 兀 f(x)ldxa例 1求由曲线 y=学 x 及直线 x=0,x=h(h>0)和 x 轴所围成的三角形 h绕 x 轴旋转而生成的立体的体积解:取 x 为积分变量,则 xe[0,h]2、平行截面面积为已知的立体的体积(截面法)由旋转体体积的计算过程可以发现如果知道该立体上垂直于一定轴的各个截面的面积,那么这个立体的体积也可以用定积分来计算30教学步骤及教学内时间分1个平面之内,以 A(x)表示过点 x 且垂直于 x 轴的截面面积.取 x 为积分变量,它的变化区间为[a,b].立体中相应于[a,b]上任一小区间[x,x+dx]的一薄片的体积近似于底面积为 A(x),高为 dx 的扁圆1柱体的体积.即:体积微元为 dV=A(x)dx于是,该立体的体积为 V=fA(x)dx例 2 计算椭圆乂+兰二 1 所围成的图形绕 x轴旋转而成的立体体积.a2b2解:这个旋转体可看作是由上半个椭圆 y=-,.a2—x2及 x 轴所围成的aA(x)=兀•(a2-x2)2aV=fA(x)dx=^^~f(a2-x2)dx=Kab2a23—a三、定积分在经济学中的应用定积分在经济学中的应用主要是已知边际函数,要求总函数的问题•已知边际成本函数 MC,边际收入函数 MR,则总成本函数 C(q),总收入函数 R(q)可以表示为图形绕 x 轴旋转所生成的立体在 x 处(-a