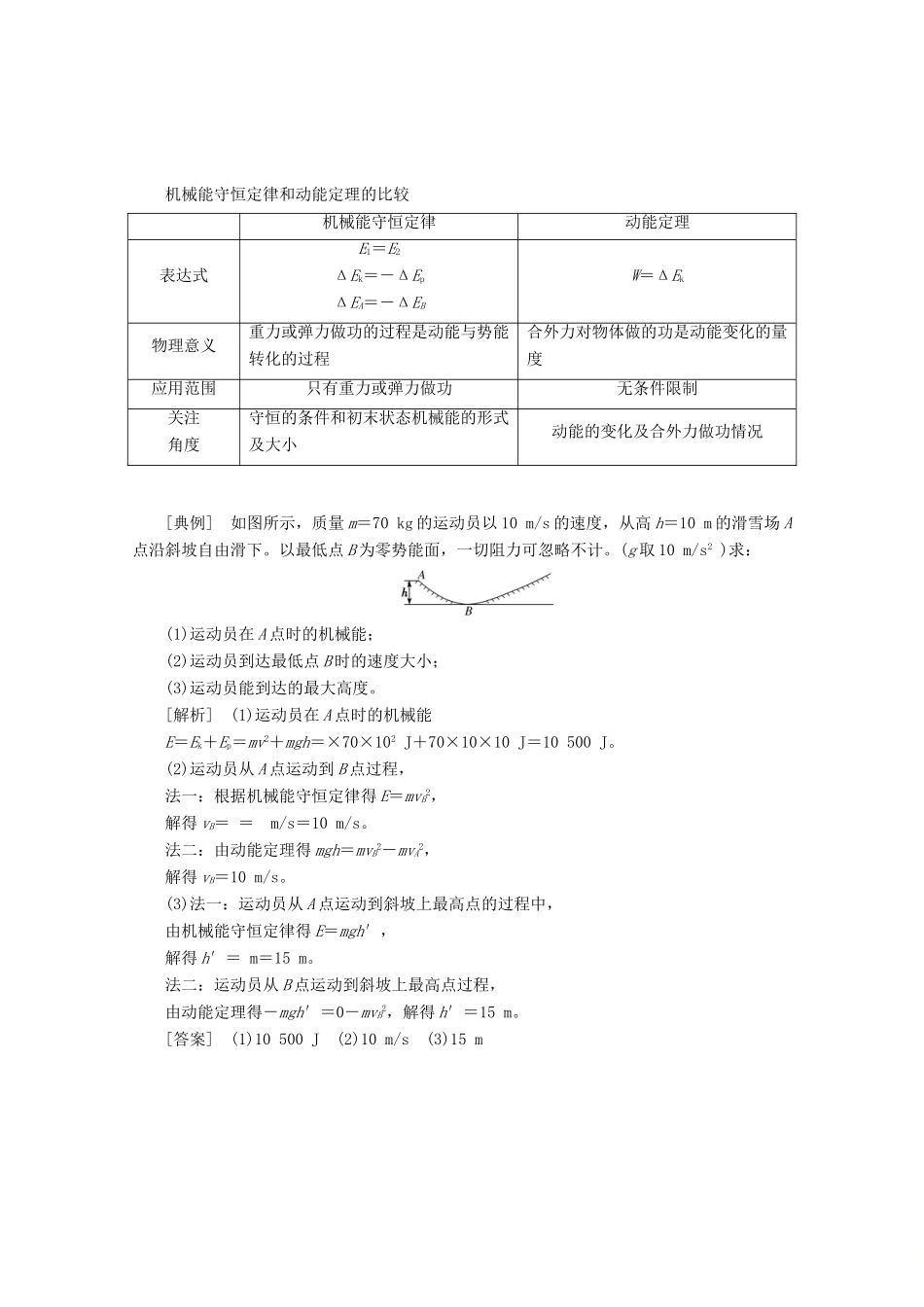
机械能守恒定律和动能定理的比较机械能守恒定律动能定理表达式E1=E2ΔEk=-ΔEpΔEA=-ΔEBW=ΔEk物理意义重力或弹力做功的过程是动能与势能转化的过程合外力对物体做的功是动能变化的量度应用范围只有重力或弹力做功无条件限制关注角度守恒的条件和初末状态机械能的形式及大小动能的变化及合外力做功情况[典例] 如图所示,质量 m=70 kg 的运动员以 10 m/s 的速度,从高 h=10 m 的滑雪场 A点沿斜坡自由滑下。以最低点 B 为零势能面,一切阻力可忽略不计。(g 取 10 m/s2 )求: (1)运动员在 A 点时的机械能;(2)运动员到达最低点 B 时的速度大小;(3)运动员能到达的最大高度。[解析] (1)运动员在 A 点时的机械能E=Ek+Ep=mv2+mgh=×70×102 J+70×10×10 J=10 500 J。(2)运动员从 A 点运动到 B 点过程,法一:根据机械能守恒定律得 E=mvB2,解得 vB= = m/s=10 m/s。法二:由动能定理得 mgh=mvB2-mvA2,解得 vB=10 m/s。(3)法一:运动员从 A 点运动到斜坡上最高点的过程中,由机械能守恒定律得 E=mgh′,解得 h′= m=15 m。法二:运动员从 B 点运动到斜坡上最高点过程,由动能定理得-mgh′=0-mvB2,解得 h′=15 m。[答案] (1)10 500 J (2)10 m/s (3)15 m