高中物理竞赛讲座讲稿：第一部分《力 物体的平衡》

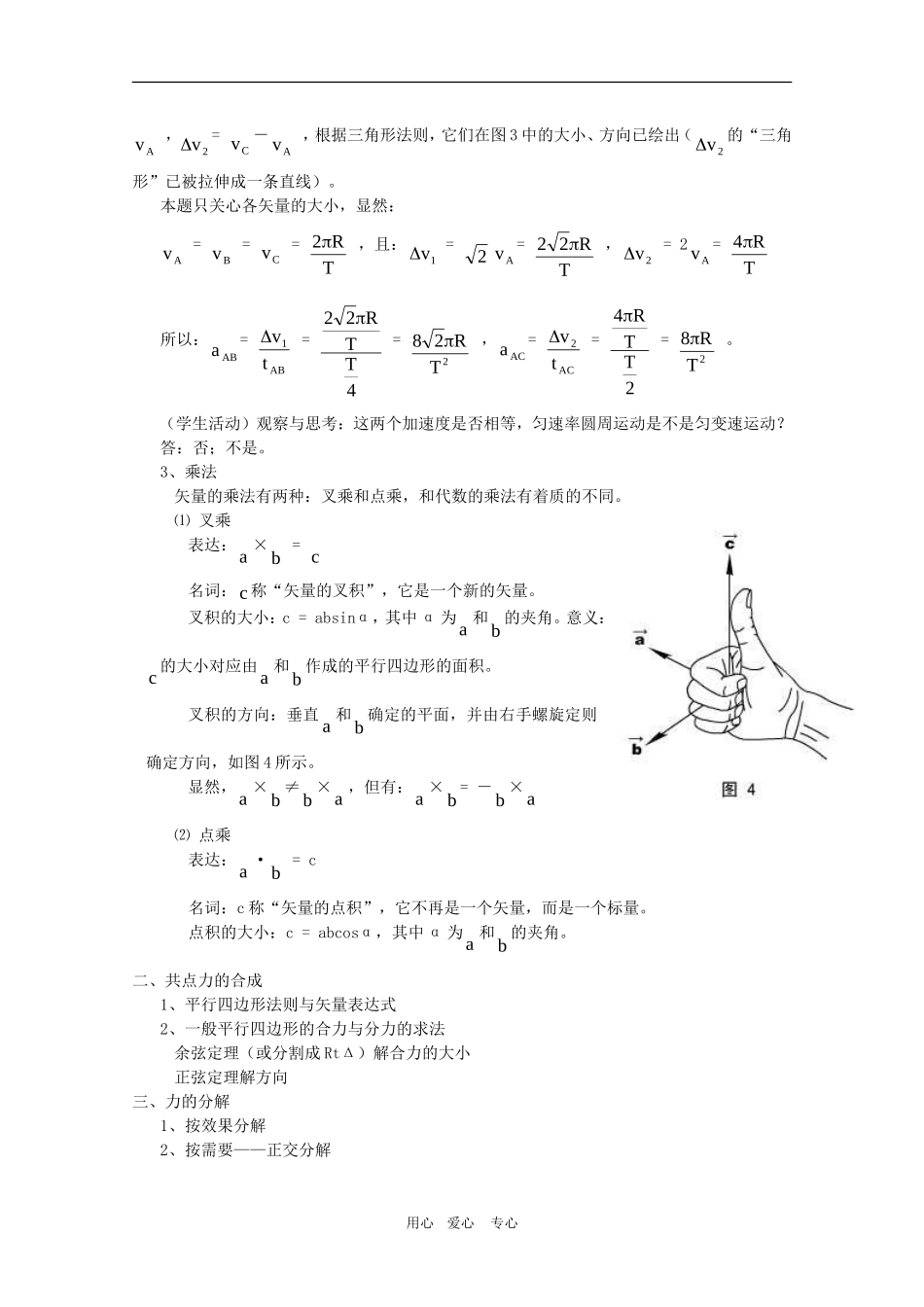
第一部分 力＆物体的平衡第一讲 力的处理一、矢量的运算1、加法表达：a + b = c 。名词：c为“和矢量”。法则：平行四边形法则。如图 1 所示。和矢量大小：c = cosab2ba22 ，其中 α 为a 和b 的夹角。和矢量方向：c在a 、b 之间，和a 夹角 β= arcsincosab2basinb222、减法表达：a = c－b 。名词：c为“被减数矢量”，b 为“减数矢量”，a 为“差矢量”。法则：三角形法则。如图 2 所示。将被减数矢量和减数矢量的起始端平移到一点，然后连接两时量末端，指向被减数时量的时量，即是差矢量。差矢量大小：a = cosbc2cb22 ，其中 θ 为c和b 的夹角。差矢量的方向可以用正弦定理求得。一条直线上的矢量运算是平行四边形和三角形法则的特例。例题：已知质点做匀速率圆周运动，半径为 R ，周期为 T ，求它在 41 T 内和在 21 T 内的平均加速度大小。解说：如图 3 所示，A 到 B 点对应 41 T 的过程，A 到 C 点对应 21 T 的过程。这三点的速度矢量分别设为Av 、Bv 和Cv 。根据加速度的定义 a = tvv0t 得：ABa= ABABtvv ，ACa= ACACtvv 由于有两处涉及矢量减法，设两个差矢量 1v= Bv －用心 爱心 专心Av ，2v= Cv －Av ，根据三角形法则，它们在图 3 中的大小、方向已绘出（2v的“三角形”已被拉伸成一条直线）。本题只关心各矢量的大小，显然：Av = Bv = Cv = TR2 ，且：1v = 2Av = TR22 ，2v = 2Av = TR4所以：ABa= AB1tv = 4TTR22 = 2TR28 ，ACa= AC2tv = 2TTR4 = 2TR8 。（学生活动）观察与思考：这两个加速度是否相等，匀速率圆周运动是不是匀变速运动？答：否；不是。3、乘法矢量的乘法有两种：叉乘和点乘，和代数的乘法有着质的不同。⑴ 叉乘表达：a ×b = c名词：c称“矢量的叉积”，它是一个新的矢量。叉积的大小：c = absinα，其中 α 为a 和b 的夹角。意义：c的大小对应由a 和b 作成的平行四边形的面积。叉积的方向：垂直 a 和 b 确定的平面，并由右手螺旋定则确定方向，如图 4 所示。显然，a ×b ≠b ×a ，但有：a ×b = －b ×a⑵ 点乘表达：a ·b = c名词：c 称“矢量的点积”，它不再是一个矢量，而是一个标...