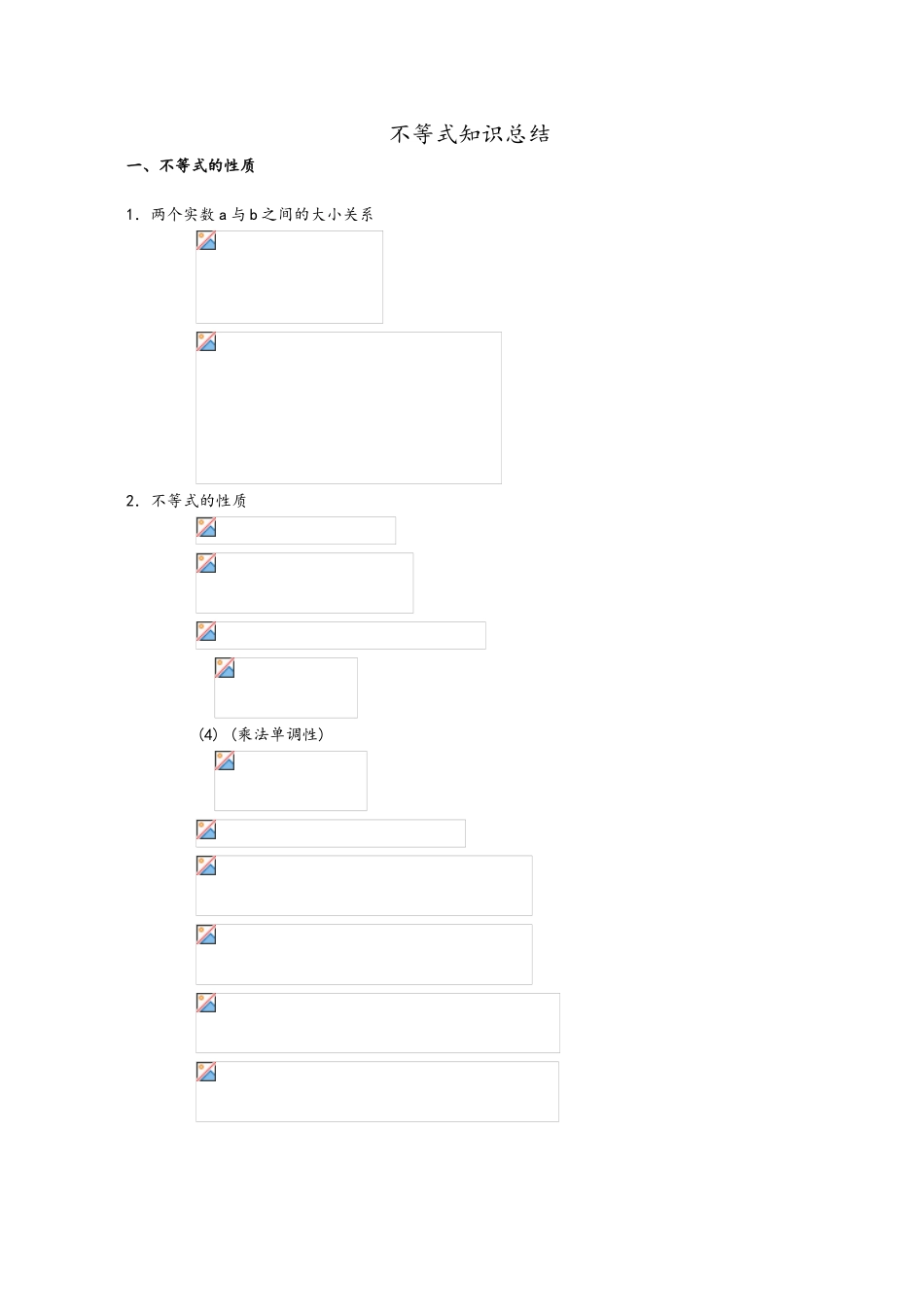
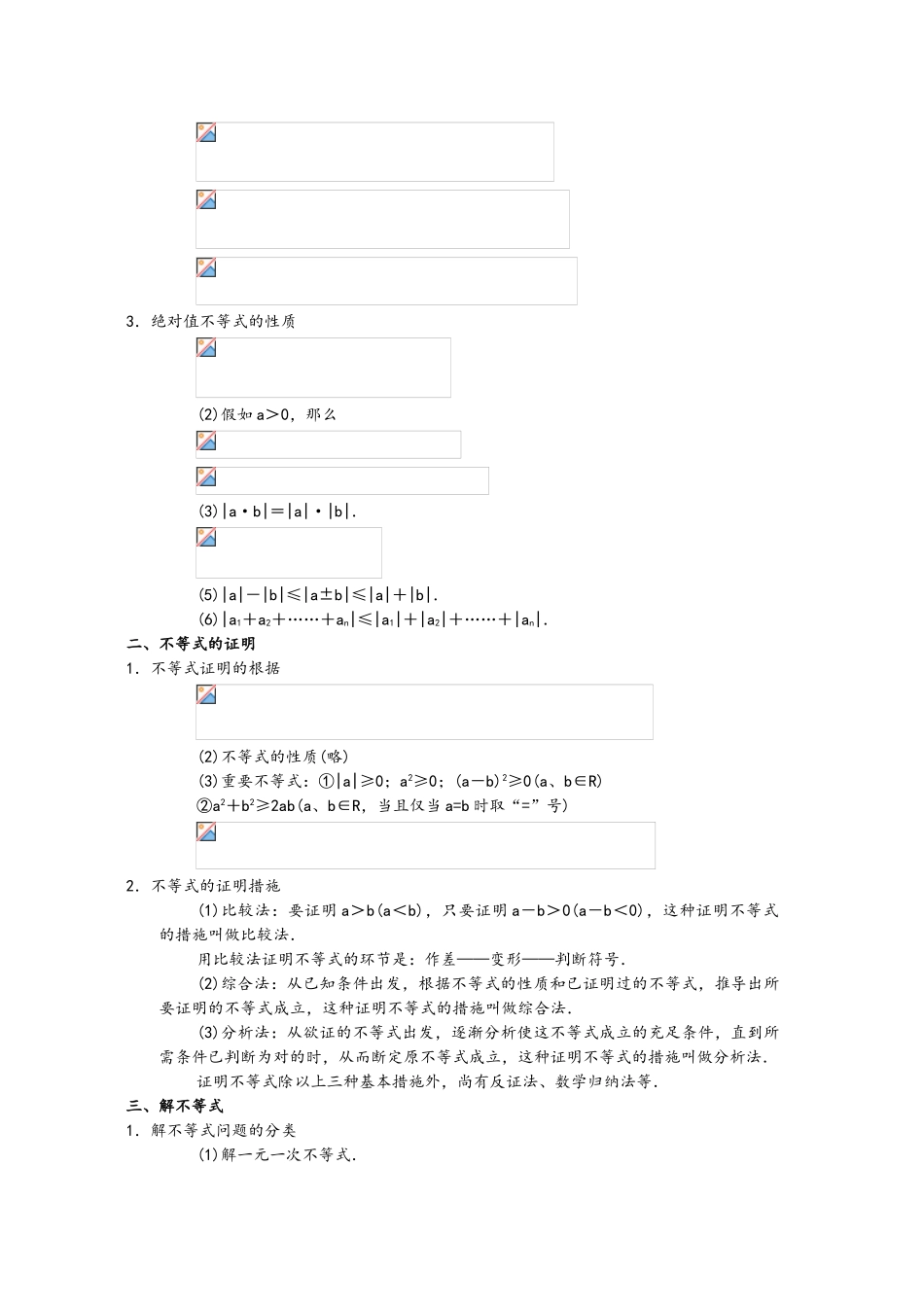
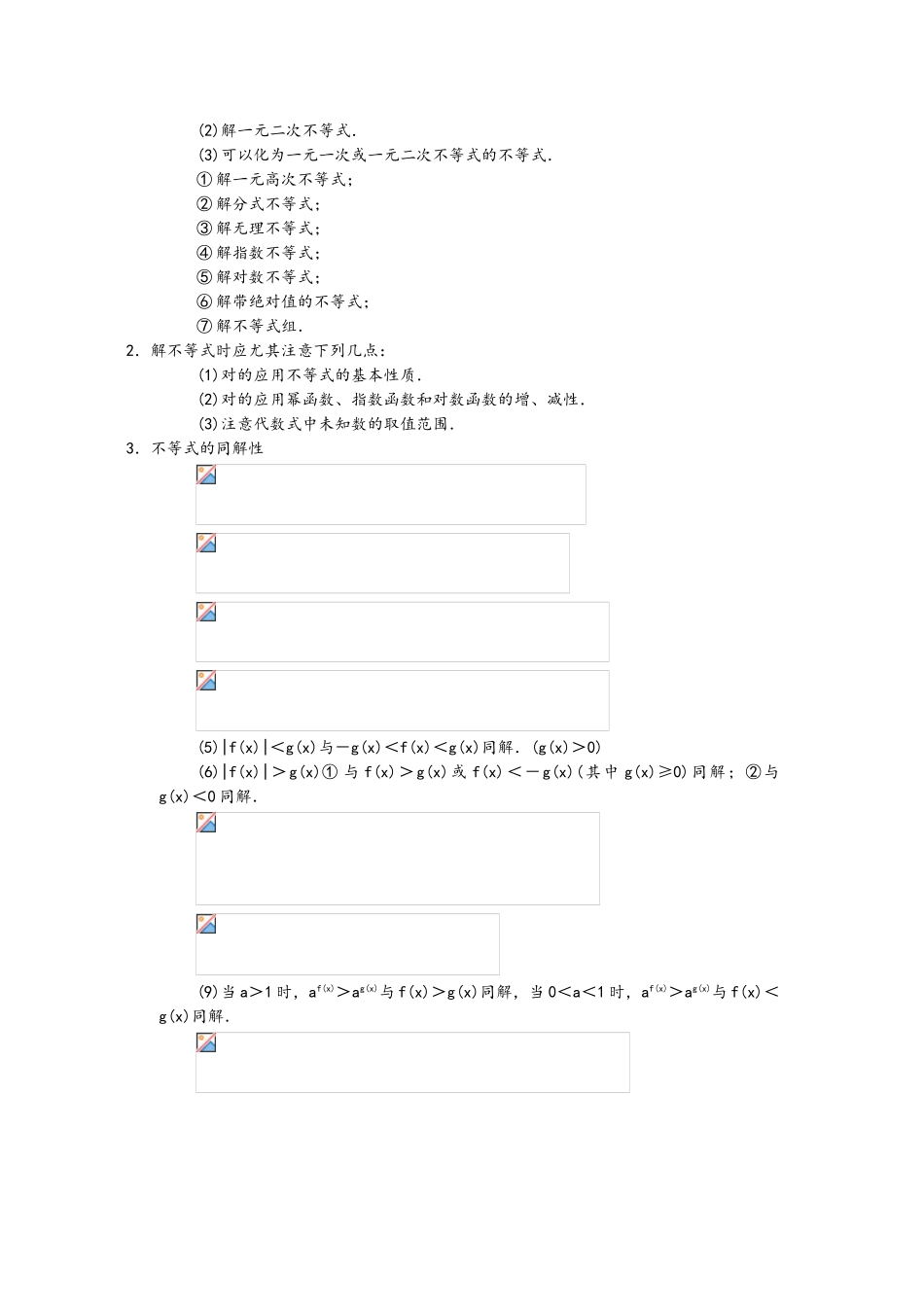
不等式知识总结一、不等式的性质1.两个实数 a 与 b 之间的大小关系2.不等式的性质(4) (乘法单调性)3.绝对值不等式的性质(2)假如 a>0,那么(3)|a·b|=|a|·|b|.(5)|a|-|b|≤|a±b|≤|a|+|b|.(6)|a1+a2+……+an|≤|a1|+|a2|+……+|an|.二、不等式的证明1.不等式证明的根据(2)不等式的性质(略)(3)重要不等式:①|a|≥0;a2≥0;(a-b)2≥0(a、b∈R)②a2+b2≥2ab(a、b∈R,当且仅当 a=b 时取“=”号)2.不等式的证明措施(1)比较法:要证明 a>b(a<b),只要证明 a-b>0(a-b<0),这种证明不等式的措施叫做比较法.用比较法证明不等式的环节是:作差——变形——判断符号.(2)综合法:从已知条件出发,根据不等式的性质和已证明过的不等式,推导出所要证明的不等式成立,这种证明不等式的措施叫做综合法.(3)分析法:从欲证的不等式出发,逐渐分析使这不等式成立的充足条件,直到所需条件已判断为对的时,从而断定原不等式成立,这种证明不等式的措施叫做分析法.证明不等式除以上三种基本措施外,尚有反证法、数学归纳法等.三、解不等式1.解不等式问题的分类(1)解一元一次不等式.(2)解一元二次不等式.(3)可以化为一元一次或一元二次不等式的不等式.① 解一元高次不等式;② 解分式不等式;③ 解无理不等式;④ 解指数不等式;⑤ 解对数不等式;⑥ 解带绝对值的不等式;⑦ 解不等式组.2.解不等式时应尤其注意下列几点:(1)对的应用不等式的基本性质.(2)对的应用幂函数、指数函数和对数函数的增、减性.(3)注意代数式中未知数的取值范围.3.不等式的同解性(5)|f(x)|<g(x)与-g(x)<f(x)<g(x)同解.(g(x)>0)(6)|f(x)|>g(x)① 与 f(x)>g(x)或 f(x)<-g(x)(其中 g(x)≥0)同解;②与g(x)<0 同解.(9)当 a>1 时,af(x)>ag(x)与 f(x)>g(x)同解,当 0<a<1 时,af(x)>ag(x)与 f(x)<g(x)同解. 单元知识总结 一、坐标法1.点和坐标建立了平面直角坐标系后,坐标平面上的点和一对有序实数(x,y)建立了一一对应的关系.2.两点间的距离公式设两点的坐标为 P1(x1,y1),P2(x2,y2),则两点间的距离特殊位置的两点间的距离,可用坐标差的绝对值表达:(1)当 x1=x2时(两点在 y 轴上或两点连线平行于 y 轴),则|P1P2|=|y2-y1|(2)当 y1=y2时(两点在 x 轴上或两点连线平行于 x 轴),则|P1P2|=|x2-x1|3.线段的定比分点(2)公式:分 P1(x1,y2)和 P2(x2,y2)连线所成的比为 λ 的...