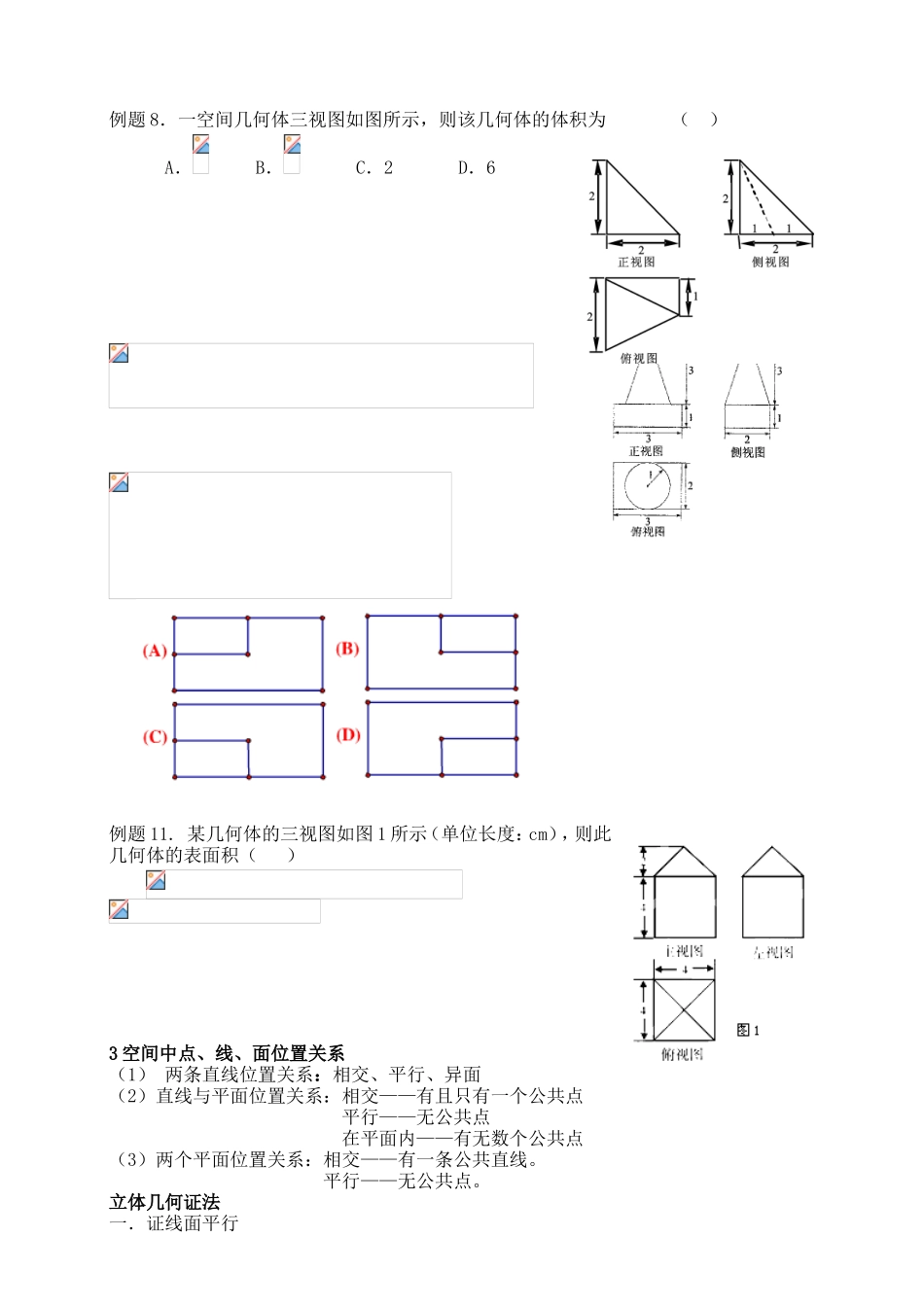
立体几何1.空间几何体的结构特征2.表面积和体积公式球表面积:(R:球的半径).球体积:.结构特征图例棱柱(1)两底面相互平行,其余各面都是平行四边形;(2)侧棱平行且相等.圆柱(1)两底面相互平行;(2)侧面的母线平行于圆柱的轴;(3)是以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体.棱锥(1)底面是多边形,各侧面均是三角形;(2)各侧面有一个公共顶点.圆锥(1)底面是圆;(2)是以直角三角形的一条直角边所在的直线为旋转轴,其余两边旋转形成的曲面所围成的几何体.棱台(1)两底面相互平行;(2)是用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分.圆台(1)两底面相互平行;(2)是用一个平行于圆锥底面的平面去截圆锥,底面和截面之间的部分.球(1)球心到球面上各点的距离相等;(2)是以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体.体积公式体积公式棱柱圆柱棱锥圆锥棱台圆台表面积相关公式表面积相关公式棱柱圆柱(r:底面半径,h:高)棱锥圆锥(r:底面半径,l:母线长)棱台圆台(r:下底半径,r’:上底半径,l:母线长)正四面体:四个面都是等边三角形.(一般可将正四面体放入正方体中讨论分析).2三视图例题6.下列四个几何体中,各几何体的三视图有且仅有两个视图相同的是()A.①②B.②③C.②④D.①③例题8.一空间几何体三视图如图所示,则该几何体的体积为()A.B.C.2D.6例题11.某几何体的三视图如图1所示(单位长度:cm),则此几何体的表面积()3空间中点、线、面位置关系(1)两条直线位置关系:相交、平行、异面(2)直线与平面位置关系:相交——有且只有一个公共点平行——无公共点在平面内——有无数个公共点(3)两个平面位置关系:相交——有一条公共直线。平行——无公共点。立体几何证法一.证线面平行例题12.如图,是正四棱柱侧棱长为1,底面边长为2,E是棱BC的中点求证:平面;例题14.如图所示,四棱锥P-ABCD底面是直角梯形,底面ABCD,E为PC的中点。PA=AD=AB=1。(1)证明:(2)证明:二.证面面平行例题15(2010诸暨)如图,四棱锥P—ABCD的底面ABCD是边长为2的菱形,,点M是棱PC的中点,N是棱PB的中点,平面ABCD,AC、BD交于点O。求证:平面OMN//平面PAD;例题16.如图,已知棱柱的底面是菱形,且面,,=1,为棱的中点,为线段的中点,(Ⅰ)求证:面;(Ⅱ)试判断直线MF与平面的位置关系,并证明你的结论;ABCDA1B1C1D1FM三.证线面垂直例题17如图所示,在直三棱柱中,,,,.证明:平面;ABCA1B1C1D例题19.(2010金华十校)一个多面体的三视图和直观图如图所示,其中正视图和俯视图均为矩形,侧视图为直角三角形,M、G分别是AB、DF的中点。(1)求证:CM平面FDM;(2)在线段AD上确定一点P,使得GP//平面FMC,并给出证明;(3)求直线DM与平面ABEF所成的角。[来源:学科网]例题20.如图,在四棱锥中,平面平面.底面为矩形,,.求证:;四.证面面垂直例题22.如图ABCD是正方形,O是正方形的中心,PO底面ABCD,E是PC的中点.求证:(1).PA//平面BDE;(2).平面PAC平面BDE.例题23.(2010浙江宁波)已知垂足为,是的中点且,,.PABDOEC(1)求证:平面平面;(2)求直线与平面所成角的正切值.五.证线线垂直(先证线面垂直):例题24.如图所示,在长方体中,,连结、.(Ⅰ)求证:;(Ⅱ)求三棱锥的体积.例题26.已知ABCD是矩形,,E、F分别是线段AB、BC的中点,面ABCD.证明:PF⊥FD;例题28.(2010浙江三校)如图,在三棱拄中,侧面,已知第26题图CDBAPEF,(Ⅰ)求证:;(Ⅱ)试在棱(不包含端点上确定一点的位置,使得;线面关系综合例题29.(2010衢州)已知直线及两个平面、,下列命题正确的是()A.若,则B.若,则C.若,则D.若,则例题32.(12苍南)已知直线,给出下列四个命题①若;②若;③若;④若其中正确命题的个数是()A.0B.1C.2D.3例题33.(2010宁波)设均为直线,其中在平面内,则“”是“且”的()(A)充分不必要条件(B)必要不充分条件(C)充分必要条件(D)既不充分也不必要条件4空间向量与立体几何1、空间直角坐标系:(1)若空间的一...