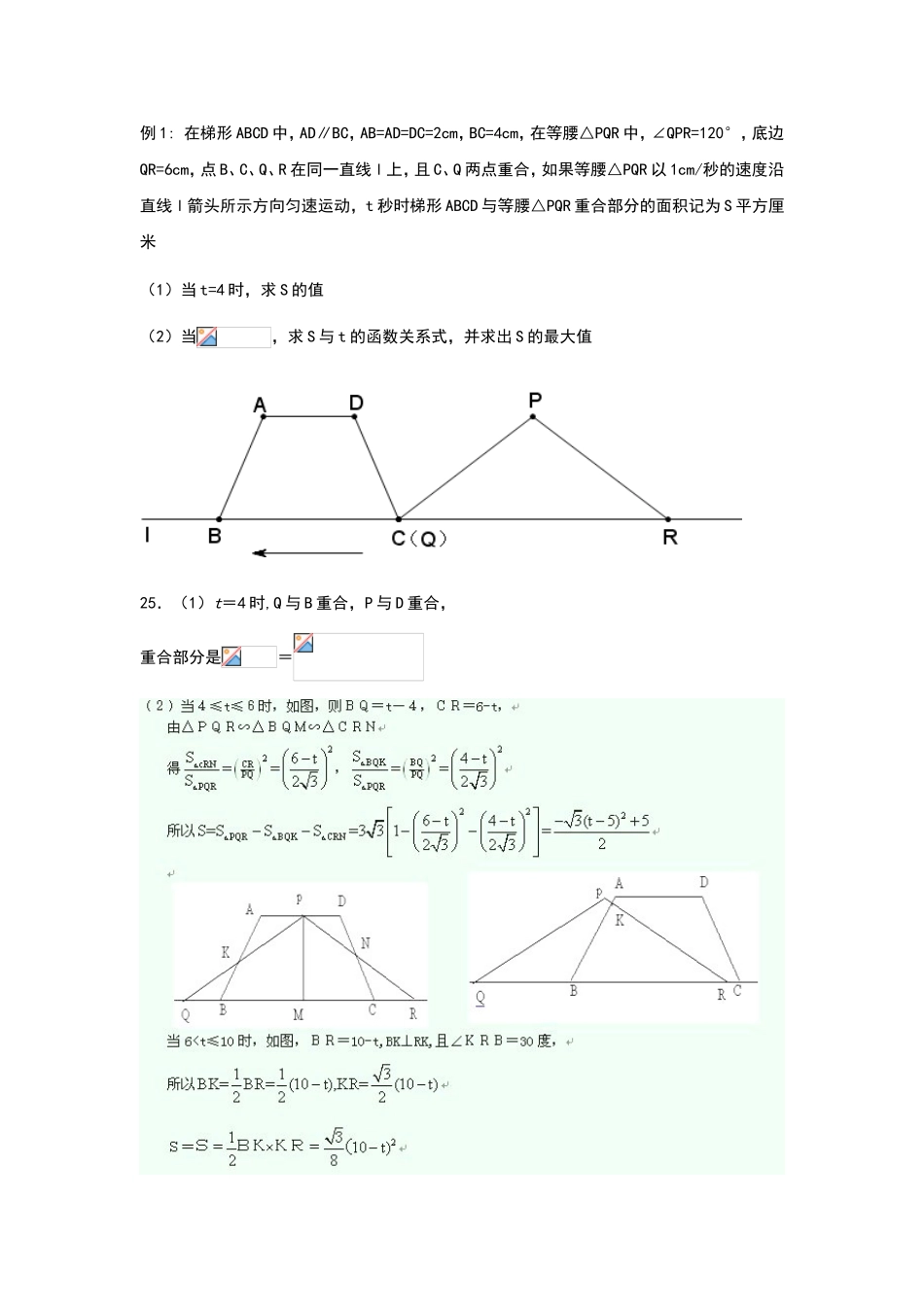
例1:在梯形ABCD中,AD∥BC,AB=AD=DC=2cm,BC=4cm,在等腰△PQR中,∠QPR=120°,底边QR=6cm,点B、C、Q、R在同一直线l上,且C、Q两点重合,如果等腰△PQR以1cm/秒的速度沿直线l箭头所示方向匀速运动,t秒时梯形ABCD与等腰△PQR重合部分的面积记为S平方厘米(1)当t=4时,求S的值(2)当,求S与t的函数关系式,并求出S的最大值25.(1)t=4时,Q与B重合,P与D重合,重合部分是=例2:如图,直线与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;(2)当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为,正方形OCMD与△AOB重叠部分的面积为S.试求S与的函数关系式并画出该函数的图象.解:(1)设点M的横坐标为x,则点M的纵坐标为-x+4(00,-x+4>0);则:MC=∣-x+4∣=-x+4,MD=∣x∣=x;∴C四边形OCMD=2(MC+MD)=2(-x+4+x)=8∴当点M在AB上运动时,四边形OCMD的周长不发生变化,总是等于8;(2)根据题意得:S四边形OCMD=MC·MD=(-x+4)·x=-x2+4x=-(x-2)2+4∴四边形OCMD的面积是关于点M的横坐标x(02,∴当t=时,S最大=………………12分例4:已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),A(10,0),B(8,),C(0,),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;(1)求∠OAB的度数,并求当点A′在线段AB上时,S关于t的函数关系式;(2)当纸片重叠部分的图形是四边形时,求t的取值范围;(3)S存在最大值吗?若存在,求出这个最大值,并求此时t的值;若不存在,请说明理由。解:(1) A,B两点的坐标分别是A(10,0)和B(8,),∴,∴当点A´在线段AB上时, ,TA=TA´,∴△ATA´是等边三角形,且,∴,,∴,当A´与B重合时,AT=AB=,所以此时。(2)当点A´在线段AB的延长线,且点P在线段AB(不与B重合)上时,纸片重叠部分的图形是四边形(如图(1),其中E是TA´与CB的交点),当点P与B重合时,AT=2AB=8,点T的坐标是(2,0)又由(1)中求得当A´与B重合时,T的坐标是(6,0)所以当纸片重叠部分的图形是四边形时,。(3)S存在最大值当时,,在对称轴t=10的左边,S的值随着t的增大而减小,∴当t=6时,S的值最大是。当时,由图,重叠部分的面积A´ABPTECOyxA´ABTECOyxPF △AEB´的高是,∴当t=2时,S的值最大是;当,即当点A´和点P都在线段AB的延长线是(如图,其中E是TA´与CB的交点,F是TP与CB的交点), ,四边形ETAB是等腰形,∴EF...