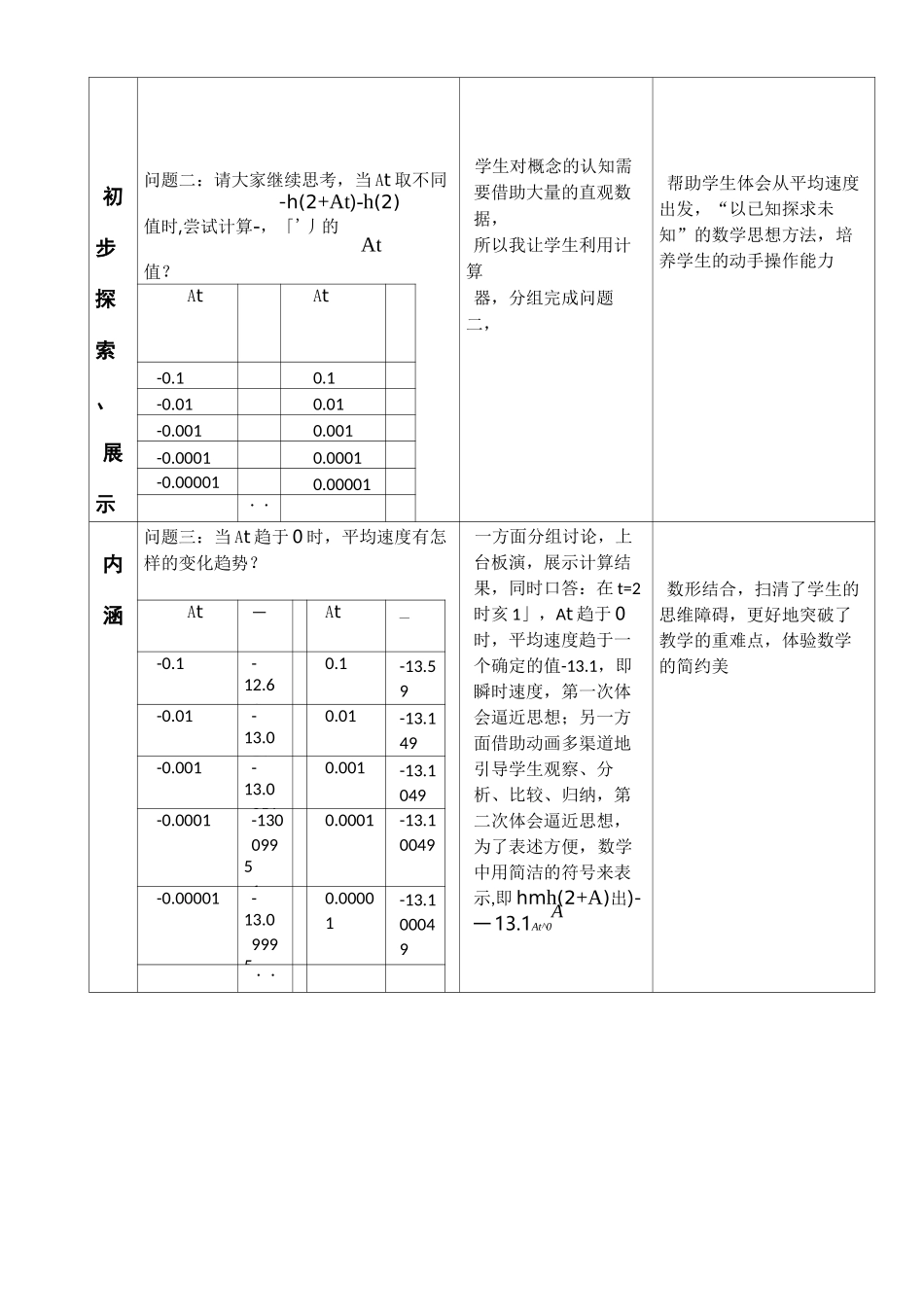
函数的平均变化率菁函数的瞬时变化率 limf(即导数)心 TO心导数概念说课稿一、教材分析导数的概念是高中新教材人教 A 版选修 2-2 第一章 1.1.2 的内容,是在学生学习了物理的平均速度和瞬时速度的背景下,以及前节课所学的平均变化率基础上,阐述了平均变化率和瞬时变化率的关系,从实例出发得到导数的概念,为以后更好地研究导数的几何意义和导数的应用奠定基础。新教材在这个问题的处理上有很大变化,它与旧教材的区别是从平均变化率入手,用形象直观的“逼近”方法定义导数。问题 1 气球平均膨胀率---瞬时膨胀率问题 2 高台跳水的平均速度一-瞬时速度根据上述教材结构与内容分析,立足学生的认知水平,制定如下教学目标和重、难点二、教学目标1、知识与技能:通过大量的实例的分析,经历由平均变化率过渡到瞬时变化率的过程,了解导数概念的实际背景,知道瞬时变化率就是导数。2、过程与方法:① 通过动手计算培养学生观察、分析、比较和归纳能力② 通过问题的探究体会逼近、类比、以已知探求未知、从特殊到一般的数学思想方法3、情感、态度与价值观:通过运动的观点体会导数的内涵,使学生掌握导数的概念不再困难,从而激发学生学习数学的兴趣.三、重点、难点>重点:导数概念的形成,导数内涵的理解>难点:在平均变化率的基础上去探求瞬时变化率,深刻理解导数的内涵通过逼近的方法,引导学生观察来突破难点四、教学设想(具体如下表)教学环节教学内容师生互动设计思路创设情景、引入新课幻灯片>回顾上节课留下的思考题:在咼台跳水运动中,运动员相对水面的咼度 h(单位:m)与起跳后的时间 t(单位:s)存在函数关系 h(t)=—4.9t2+6.5t+10.计算运动员在 0结合跳水问题,明确瞬时速度的定义问题一:请大家思考如何求运动员...