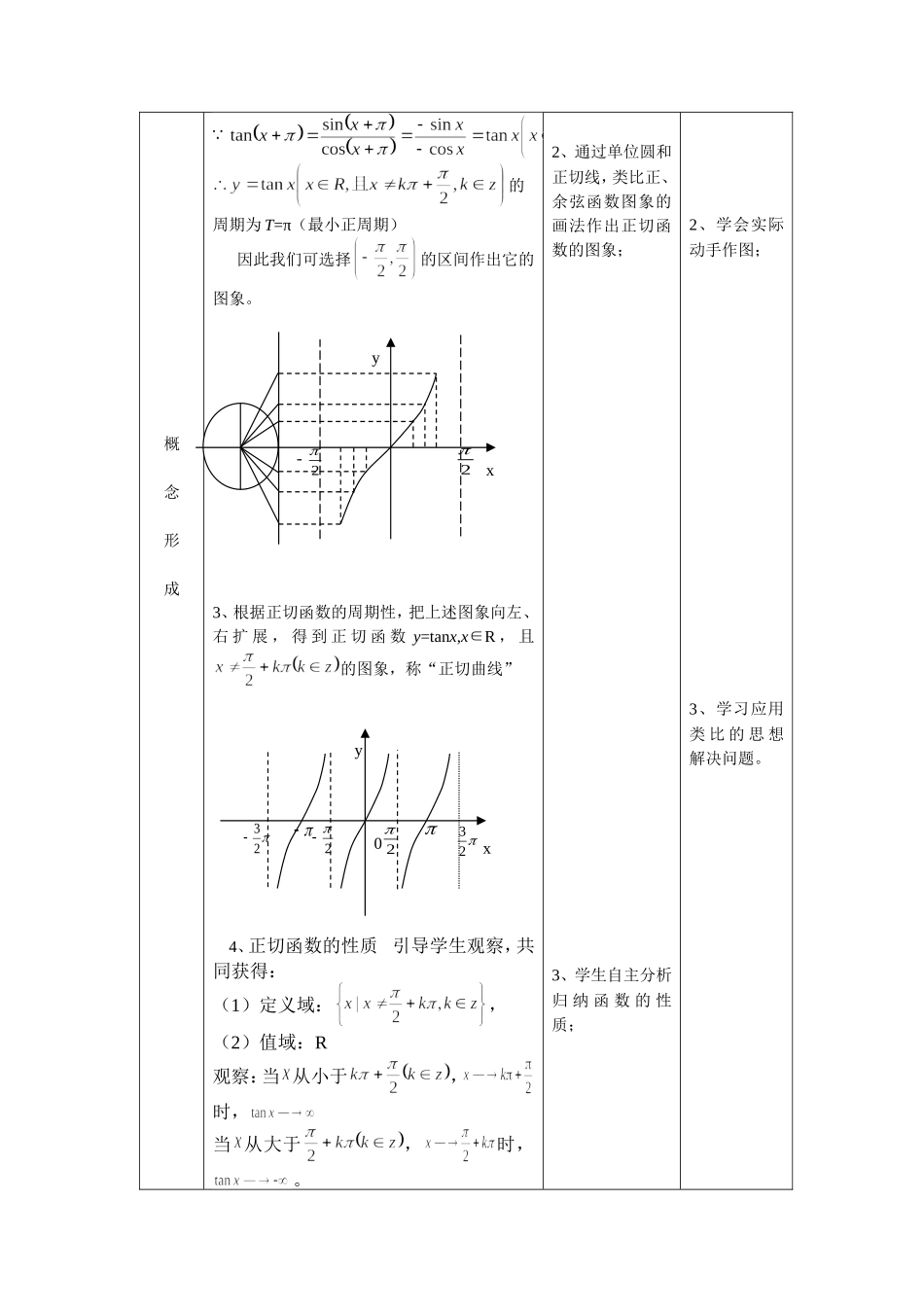
1.3.2(第二课时)正切函数的图象和性质一、教学目标1.知识目标(1)了解利用正切线画出正切函数图象的方法;(2)了解正切曲线的特征;(3)了解正切函数的性质。2、能力目标理解并掌握利用正切函数的图象和性质解题3、情感目标(1)掌握“类比”的学习方法;(2)渗透数形结合,换元法等基本数学思想方法。二、教学重、难点重点:正切函数的图象形状及其主要性质(包括定义域、值域、周期性、奇偶性和单调性)。难点:利用正切线画出函数的图象,并使直线确实称为此图象的两条渐进线。关键:充分利用图形讲清正切曲线的特性,通过一定的训练使学生正确了解图象性质(例如定义域必须去掉各点,值域无最大值、最小值,周期是 π,单调性表现为在每一单调区间内只增不减等)。三、教学方法 结合本节内容的特征,主要采用启发诱导式教学方式,让学生自主地去探求知识。适当借助多媒体等教学辅助手段。四、教学过程教学环节教学内容师生互动设计意图复习引入1、在单位圆中复习正切线(AT)的定义;2、回忆正弦函数图象的作法(几何法);3、由前面的知识可知:一个周期函数的作图问题,只需作出它在一个周期内的函数图象,然后通过左右扩展即可得到它在整个定义域内的图象。如果正切函数也是周期函数的话,我们就可以这么做,那么正切函数是周期函数吗?如果是,最小正周期又是多少呢?1、教学提问,学生回答或演练;2、配合多媒体分析问题的实质,让学生归纳总结出相应的结论。1、鼓励学生提 炼 解 决 问题 和 研 究 问题 的 一 般 方法,养成获取新 知 识 的 习惯;2、加强学生的实践经验。1、首先考虑定义域:2、为了研究方便,再考虑一下它的周期: 1、师生共同寻找研究图象的常见的参数:定义域、周期等;1、让学生学会分析、解决问 题 的 一 般方法;概念形成 的周期为 T=π(最小正周期)因此我们可选择的区间作出它的图象。3、根据正切函数的周期性,把上述图象向左、右 扩 展 , 得 到 正 切 函 数 y=tanx,x∈R , 且的图象,称“正切曲线”4、正切函数的性质 引导学生观察,共同获得:(1)定义域:,(2)值域:R 观察:当 从小于,时,当 从大于,时,。2、通过单位圆和正切线,类比正、余弦函数图象的画法作出正切函数的图象;3、学生自主分析归 纳 函 数 的 性质;2、学会实际动手作图;3、学习应用类 比 的 思 想解决问题。xy222322230yx(3)周期性:T=π(...