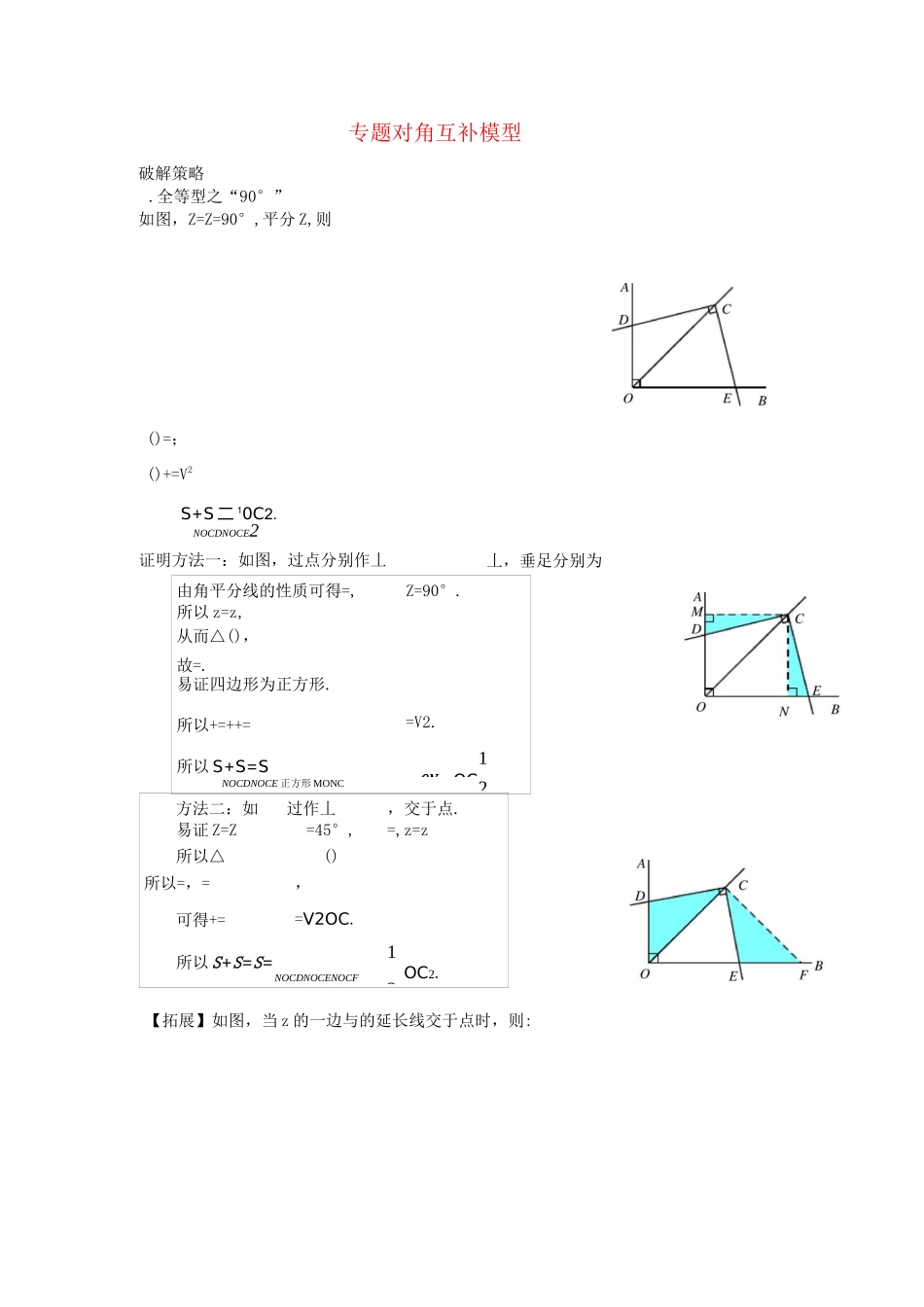
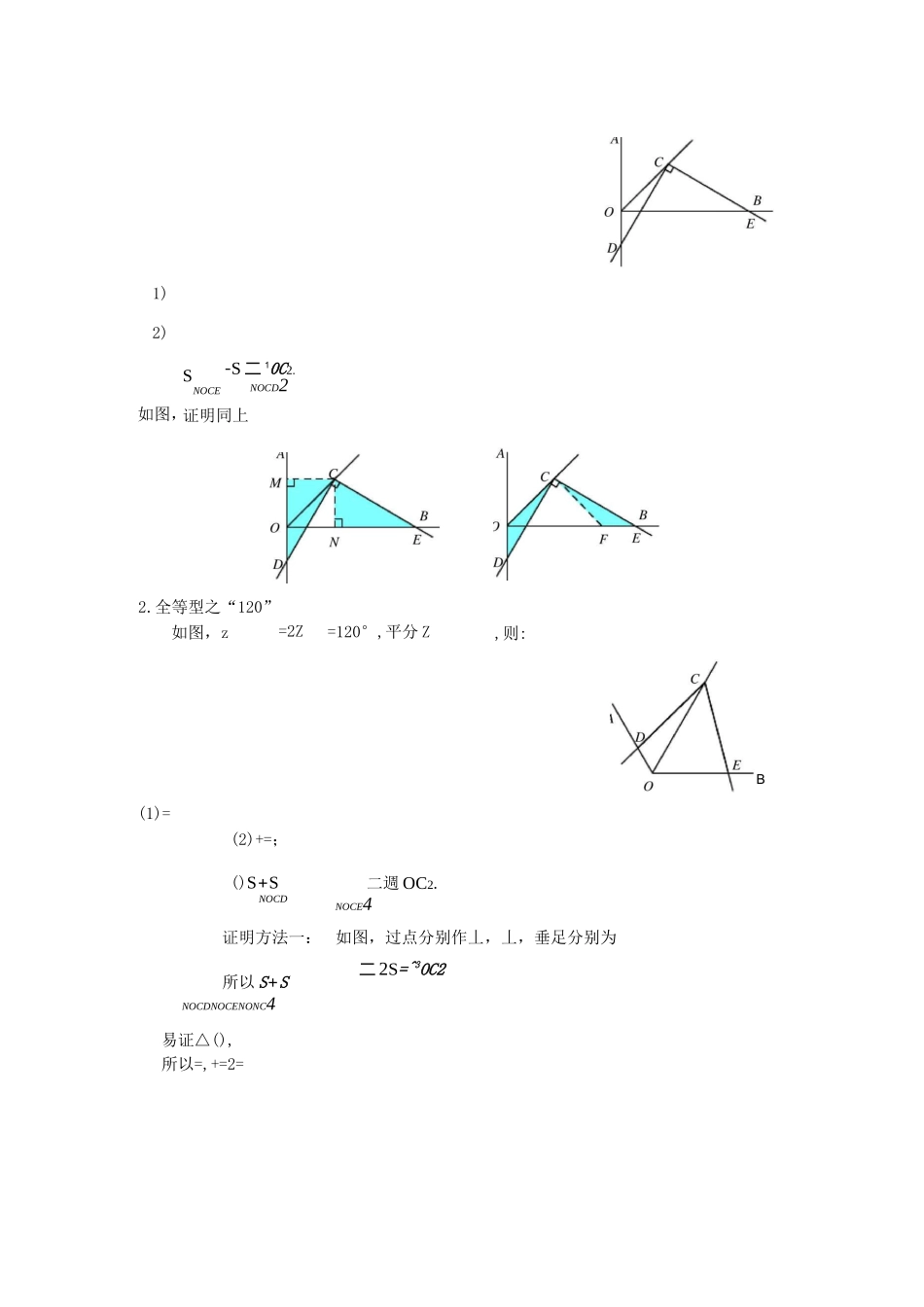
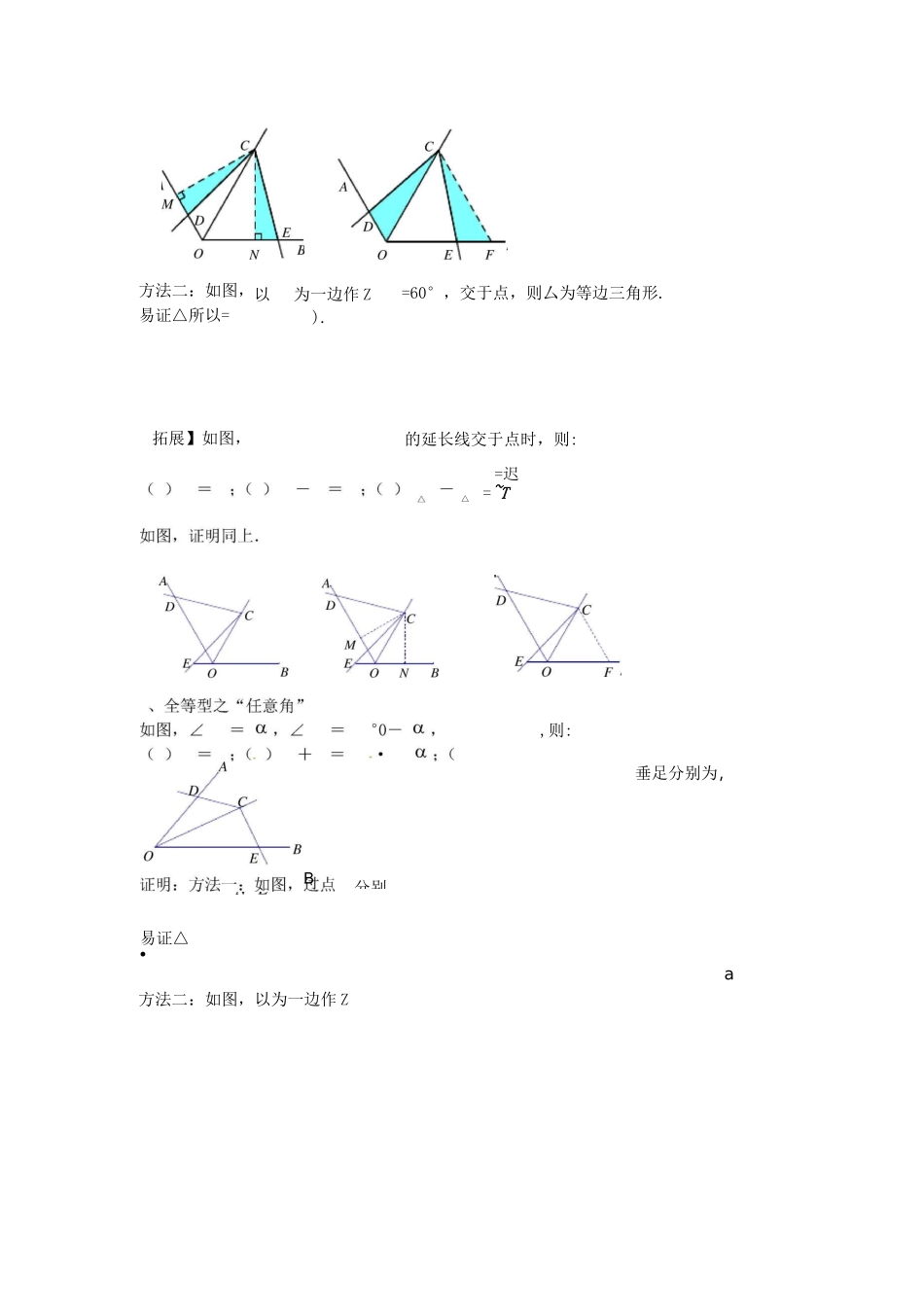
专题对角互补模型破解策略.全等型之“90°”如图,Z=Z=90°,平分 Z,则()=;()+=V2S+S 二 10C2.NOCDNOCE2证明方法一:如图,过点分别作丄丄,垂足分别为由角平分线的性质可得=,Z=90°.所以 z=z,从而△(),故=.易证四边形为正方形.所以+=++==V2.所以 S+S=S1=ON2=OC2.NOCDNOCE 正方形 MONC2方法二:如图,过作丄,交于点.易证 Z=Z=45°,=,z=z所以△()所以=,=,可得+==V2OC.所以 S+S=S=NOCDNOCENOCF1OC2.2【拓展】如图,当 z 的一边与的延长线交于点时,则:(1)=(2)+=;()S+S二週 OC2.NOCDNOCE4证明方法一:如图,过点分别作丄,丄,垂足分别为所以 S+S二 2S=^3OC2NOCDNOCENONC4易证△(),所以=,+=2=1)2)如图,SNOCE证明同上-S 二 10C2.NOCD22.全等型之“120”=2Z如图,z=120°,平分 Z,则:B垂足分别为,a方法二:如图,以为一边作 Z分别以方法二:如图,易证△所以=拓展】如图,为一边作 Z).=60°,交于点,则厶为等边三角形.的延长线交于点时,则:△=迟=~T,则:B易证△•B,+•:△+【拓展】如图,当Z()=;()如图,证明同上・a的一边与a的延长线交于点a;()—△时,则:anaBBBZ丄=•tana垂足分别为、易证△CECN=CM=tana,即方法二:~MD~~CD作丄,交于点.=•tana如图,过点B•tan【拓展】如图,当的一边的延长线交于点时,则=FECECFOD=CD=CO=tan,即.*.Z=Z,故=・tarf^如图,证明同上.如图,过点分别向 Z由题意可得 Z=Z的两边作垂线,垂足分别为、方法三:如图,连接例题讲解例、已知△是 O 的内接二角形,=,在 Z所对弧上任取一点,连接()如图,那么+与之间的数量关系是什么?()如图,若 Z=d易证△•:+如图,=v'3a2=z,所以,交+a2•的对角线上滑动,并使其于占J 八、、-•所以2例如图,将一个直角三角板的直角顶点一条直角边始终经过点,另一条直角边与⑴求证⑵ 如图⑶如图放在正方形相交于点•,将⑴中的正方形变为矩形,其余不变,且,在⑵的条件下,当D滑动到的延长线上时,=,求:的值;的值是否发生变化?解则△故过占C丄,丄D⑴ 如图,分别作°,由已知条件可得 z,垂足分别为,=°,所以 z=z⑵ 如图,过点分别作丄,丄,垂足分别为,.则〃,〃所以△,△PMBPPN 可得==所以PMAD5ADBDCDPNCD4易证△,所以APPM_5.PEPN4的值不变.如图,进阶训练.如图,四边形直角,另一条对角线被对角线分为等腰△的长度为,则四边形和△,其中 Z 和 Z 都是的面积为第 1 题图答案:四边形【提示】易证、的结论可得四边形的面积为.、、四点共...