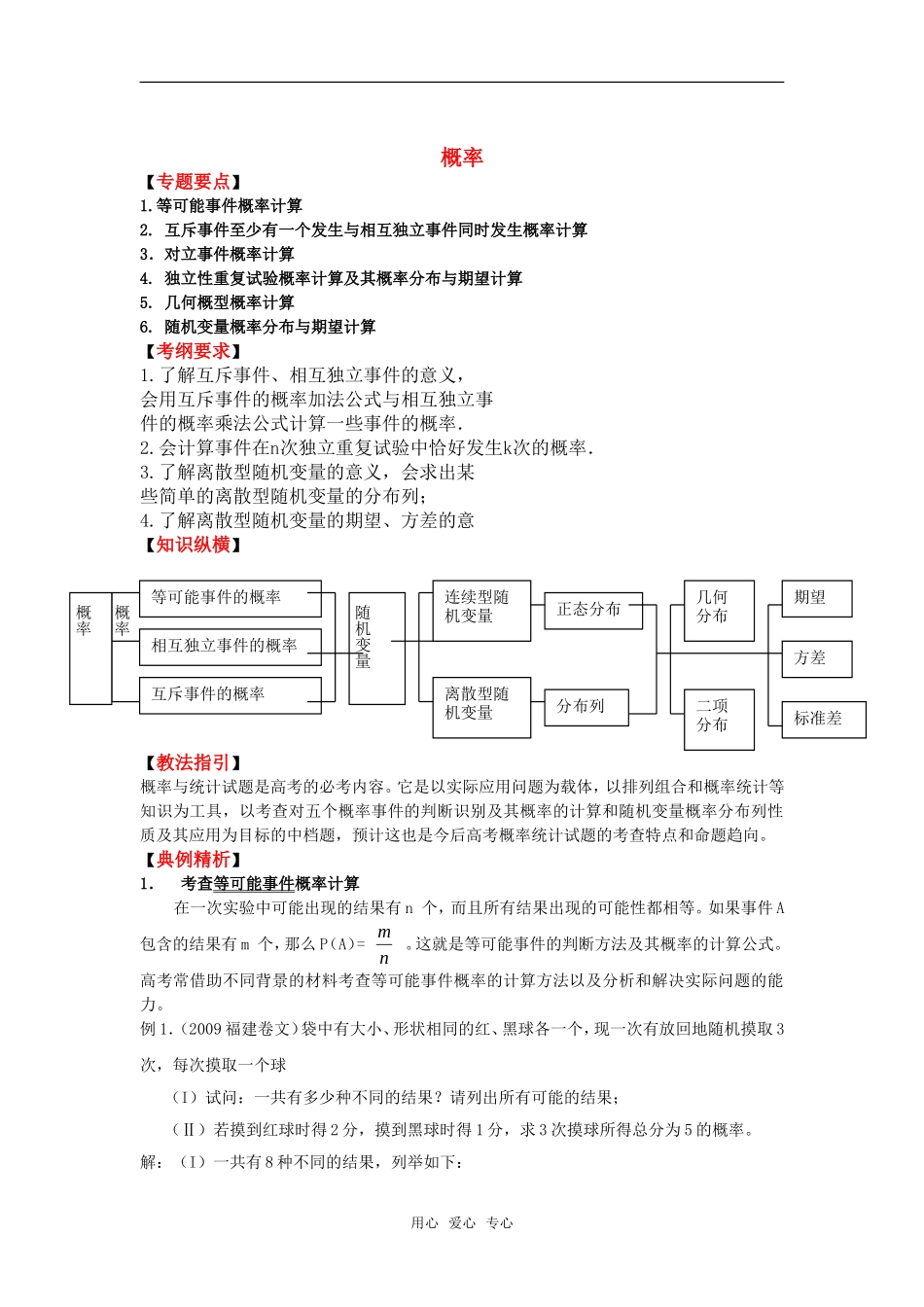
概率【专题要点】1.等可能事件概率计算2. 互斥事件至少有一个发生与相互独立事件同时发生概率计算3.对立事件概率计算4. 独立性重复试验概率计算及其概率分布与期望计算5. 几何概型概率计算6. 随机变量概率分布与期望计算【考纲要求】1.了解互斥事件、相互独立事件的意义,会用互斥事件的概率加法公式与相互独立事件的概率乘法公式计算一些事件的概率.2.会计算事件在n次独立重复试验中恰好发生k次的概率.3.了解离散型随机变量的意义,会求出某些简单的离散型随机变量的分布列;4.了解离散型随机变量的期望、方差的意【知识纵横】【教法指引】概率与统计试题是高考的必考内容。它是以实际应用问题为载体,以排列组合和概率统计等知识为工具,以考查对五个概率事件的判断识别及其概率的计算和随机变量概率分布列性质及其应用为目标的中档题,预计这也是今后高考概率统计试题的考查特点和命题趋向。【典例精析】1. 考查等可能事件概率计算在一次实验中可能出现的结果有 n 个,而且所有结果出现的可能性都相等。如果事件 A包含的结果有 m 个,那么 P(A)= nm 。这就是等可能事件的判断方法及其概率的计算公式。高考常借助不同背景的材料考查等可能事件概率的计算方法以及分析和解决实际问题的能力。例 1.(2009 福建卷文)袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取 3次,每次摸取一个球 (I)试问:一共有多少种不同的结果?请列出所有可能的结果; (Ⅱ)若摸到红球时得 2 分,摸到黑球时得 1 分,求 3 次摸球所得总分为 5 的概率。解:(I)一共有 8 种不同的结果,列举如下:用心 爱心 专心等可能事件的概率相互独立事件的概率互斥事件的概率随机变量概率概率连续型随机变量离散型随机变量正态分布分布列几何分布二项分布期望方差标准差 (红、红、红、)、(红、红、黑)、(红、黑、红)、(红、黑、黑)、(黑、红、红)、(黑、红、黑)(黑、黑、红)、(黑、黑、黑) (Ⅱ)记“3 次摸球所得总分为 5”为事件 A 事件 A 包含的基本事件为:(红、红、黑)、(红、黑、红)、(黑、红、红)事件 A 包含的基本事件数为 3 由(I)可知,基本事件总数为 8,所以事件 A 的概率为3( )8P A . 例 2.(2009 安徽卷理)考察正方体 6 个面的中心,甲从这 6 个点中任意选两个点连成直线,乙也从这 6 个点中任意选两个点连成直线,则所得的两条直线相互平行但不重...