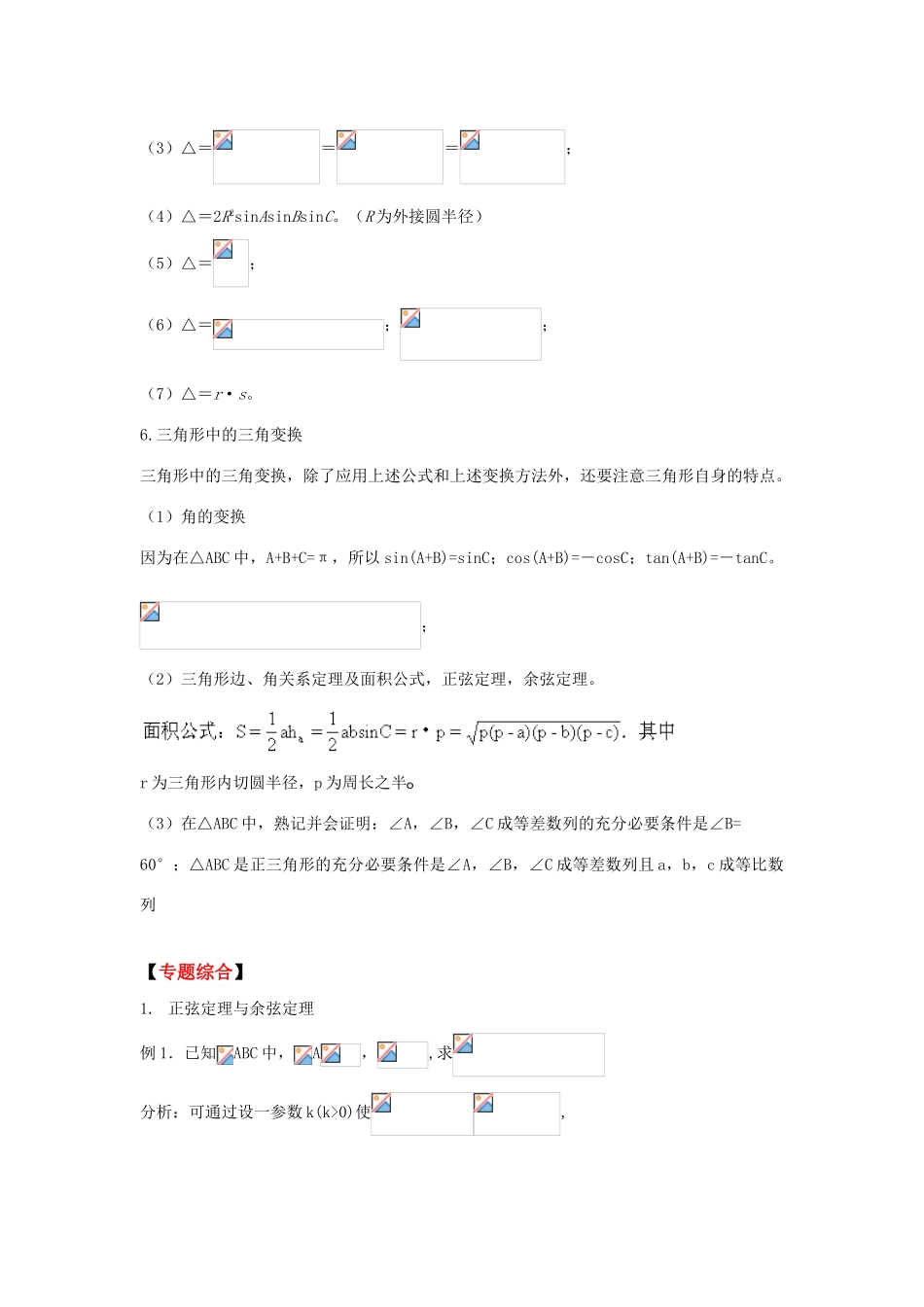
解三角形【学法导航】处理三角形问题,必须结合三角形全等的判定定理理解斜三角形的四类基本可解型,特别要多角度(几何作图,三角函数定义,正、余弦定理,勾股定理等角度)去理解“边边角”型问题可能有两解、一解、无解的三种情况,根据已知条件判断解的情况,并能正确求解1.三角形中的边角关系三角形内角和等于 180°;三角形中任意两边之和大小第三边,任意两边之差小于第三边;三角形中大边对大角,小边对小角;正弦定理中,a=2R·sin A ,b=2R·sin B ,c=2R·sin C ,其中 R 是△ ABC 外接圆半径 .在余弦定理中:2bccosA=.三角形的面积公式有:S=ah,S=absinC,S=其中,h 是 BC 边上高 ,P 是半周长.2.利用正、余弦定理及三角形面积公式等解任意三角形已知两角及一边,求其它边角,常选用正弦定理.已知两边及其中一边的对角,求另一边的对角,常选用正弦定理.已知三边,求三个角,常选用余弦定理. 已知两边和它们的夹角,求第三边和其他两个角,常选用余弦定理.已知两边和其中一边的对角,求第三边和其他两个角,常选用正弦定理.3.利用正、余弦定理判断三角形的形状常用方法是:①化边为角;②化角为边.4.解斜三角形在实际中的运用5.三角形的面积公式:(1)△=aha=bhb=chc(ha、hb、hc分别表示 a、b、c 上的高);(2)△=absinC=bcsinA=acsinB;(3)△===;(4)△=2R2sinAsinBsinC。(R 为外接圆半径)(5)△=;(6)△=;;(7)△=r·s。6.三角形中的三角变换三角形中的三角变换,除了应用上述公式和上述变换方法外,还要注意三角形自身的特点。(1)角的变换因为在△ABC 中,A+B+C=π,所以 sin(A+B)=sinC;cos(A+B)=-cosC;tan(A+B)=-tanC。;(2)三角形边、角关系定理及面积公式,正弦定理,余弦定理。r 为三角形内切圆半径,p 为周长之半(3)在△ABC 中,熟记并会证明:∠A,∠B,∠C 成等差数列的充分必要条件是∠B=60°;△ABC 是正三角形的充分必要条件是∠A,∠B,∠C 成等差数列且 a,b,c 成等比数列【专题综合】1. 正弦定理与余弦定理例 1.已知ABC 中,A,,求分析:可通过设一参数 k(k>0)使,证明出解:设 则有,,从而==又,所以=2小结: ABC 中,等式恒成立。[补充练习]已知ABC 中,,求(答案:1:2:3)(归纳总结):(1)定理的表示形式:;或,,(2)正弦定理的应用范围:①已知两角和任一边,求其它两边及一角;② 已知两边和其中一边对角,求另一边的对角...