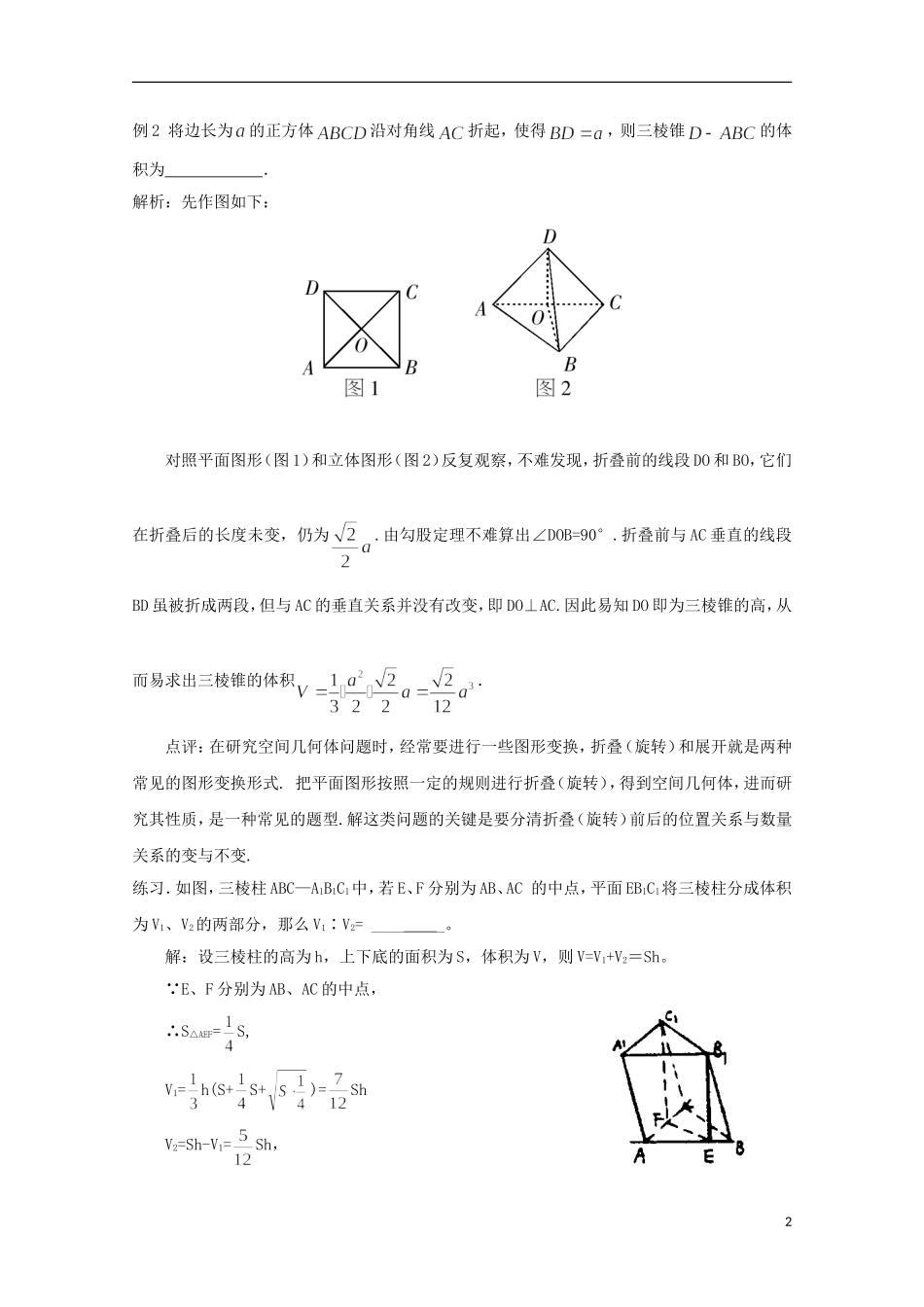
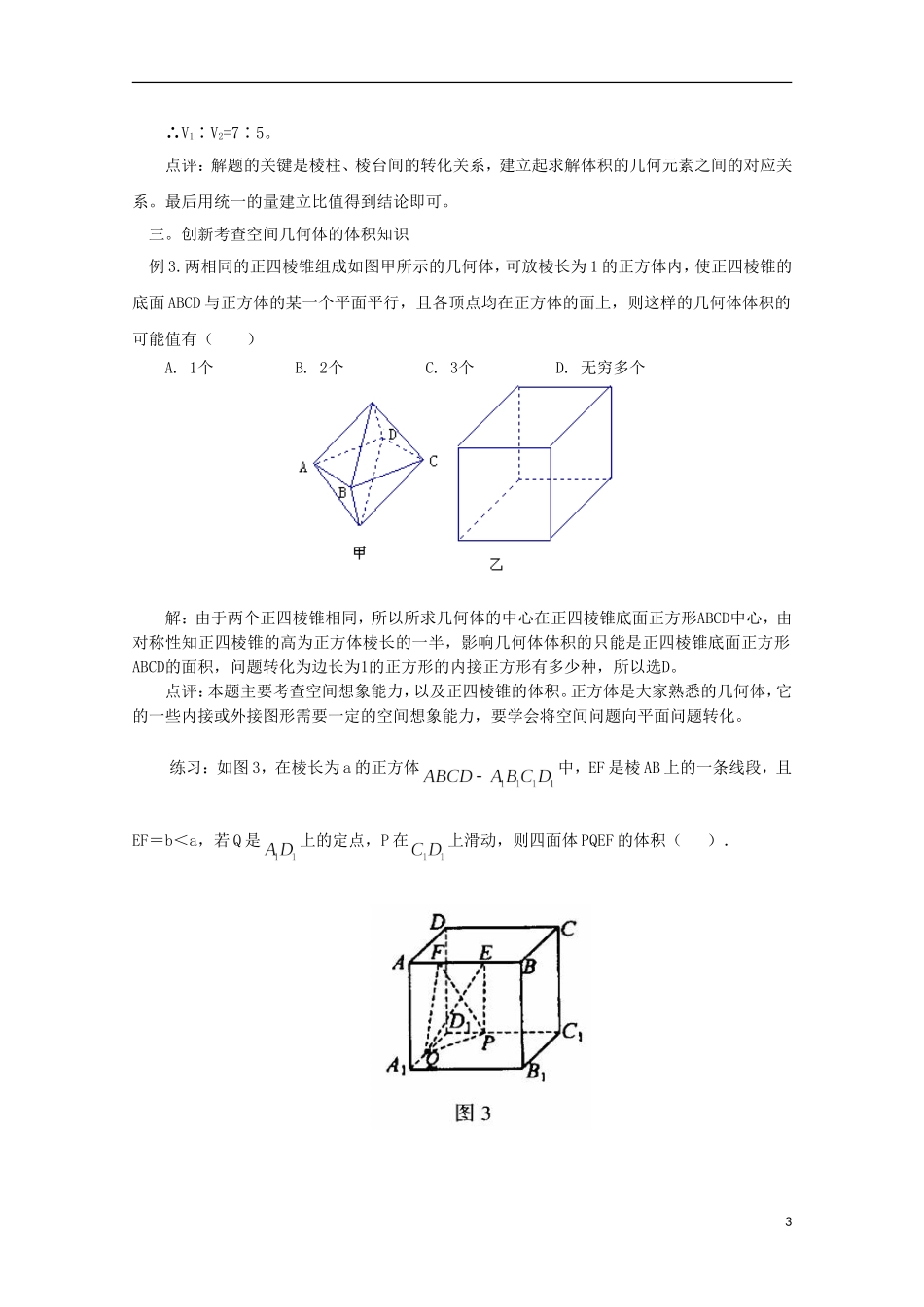
例析空间几何体的体积问题近几年来,立体几何高考命题形式比较稳定,题目难易适中,而选择题、填空题又经常研究空间几何体的几何特征和体积、表面积。体积的计算,是定量研究几何体的重要内容与方法.对一些常用公式要牢记,包括柱体、锥体和球体的体积公式。下面给出一些典型例题希望对大家有帮助。一直接考查体积公式例 1:养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12M ,高4M ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4M(高不变);二是高度增加4M (底面直径不变)。(1)分别计算按这两种方案所建的仓库的体积;(2)分别计算按这两种方案所建的仓库的表面积;(3)哪个方案更经济些? 解:(1)如果按方案一,仓库的底面直径变成16M ,则仓库的体积23111162564()3323VShM 如果按方案二,仓库的高变成8M ,则仓库的体积23211122888()3323VShM (2)如果按方案一,仓库的底面直径变成16M ,半径为8M 。 棱锥的母线长为22844 5l 则仓库的表面积218 4 532 5 ()SM 如果按方案二,仓库的高变成8M 。 棱锥的母线长为228610l 则仓库的表面积226 1060 ()SM (3)21VV ,21SS 方案二比方案一更加经济练习:正四棱锥底面边长为 4,侧棱长为 3,则其体积为 .解 : 如 图 , 在 △ OPA 中 , 因 为 , 所 以 正 四 棱 锥 的 高 为 ,故正四棱锥的体积为 从而应填.二 巧妙变形考查体积公式1例 2 将边长为的正方体沿对角线折起,使得,则三棱锥的体积为 .解析:先作图如下: 对照平面图形(图 1)和立体图形(图 2)反复观察,不难发现,折叠前的线段 DO 和 BO,它们在折叠后的长度未变,仍为.由勾股定理不难算出∠DOB=90°.折叠前与 AC 垂直的线段BD 虽被折成两段,但与 AC 的垂直关系并没有改变,即 DO⊥AC.因此易知 DO 即为三棱锥的高,从而易求出三棱锥的体积.点评:在研究空间几何体问题时,经常要进行一些图形变换,折叠(旋转)和展开就是两种常见的图形变换形式. 把平面图形按照一定的规则进行折叠(旋转),得到空间几何体,进而研究其性质,是一种常见的题型.解这类问题的关键是要分清折叠(旋转)前后的位置关系与数量关系的变与不变...