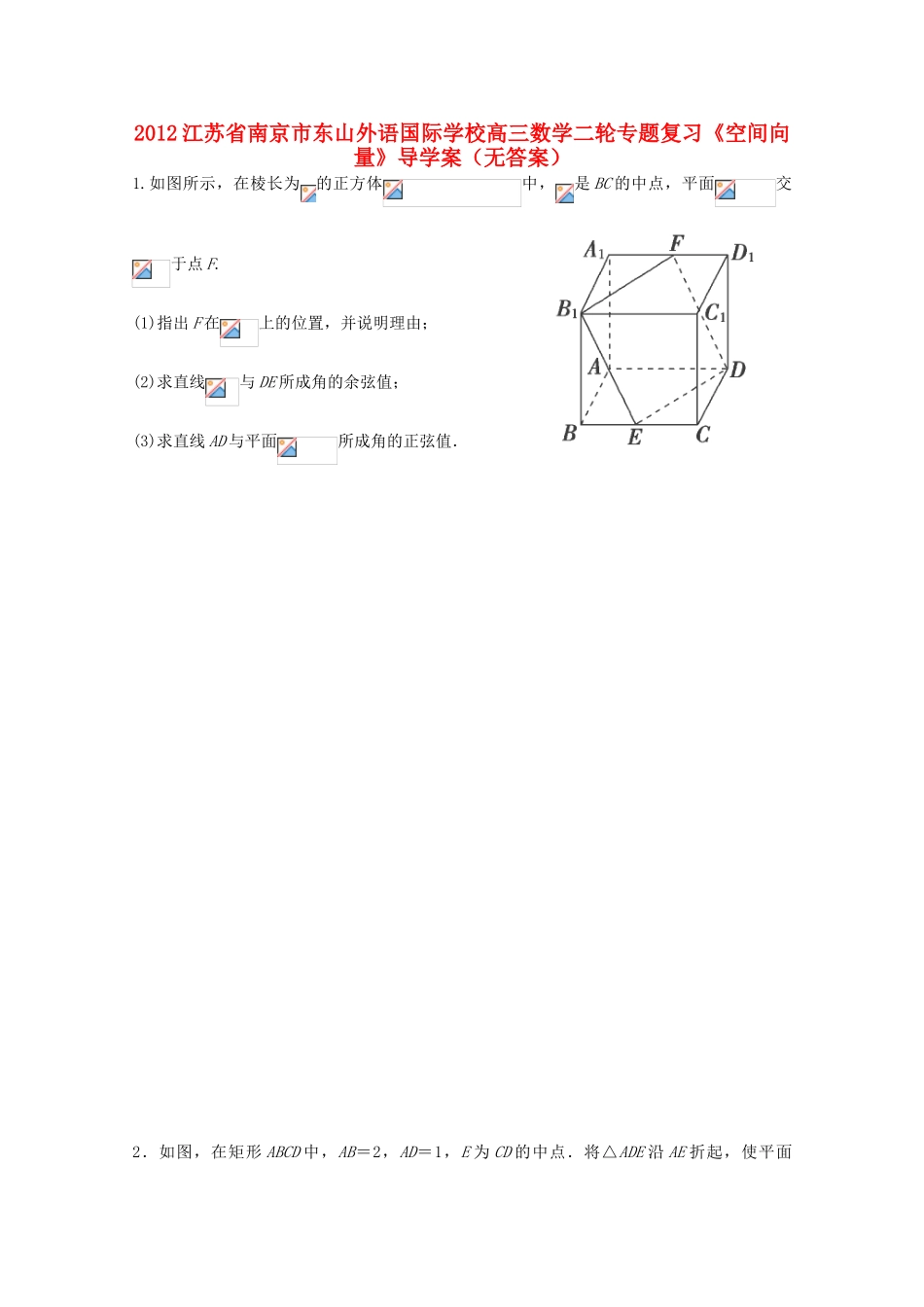
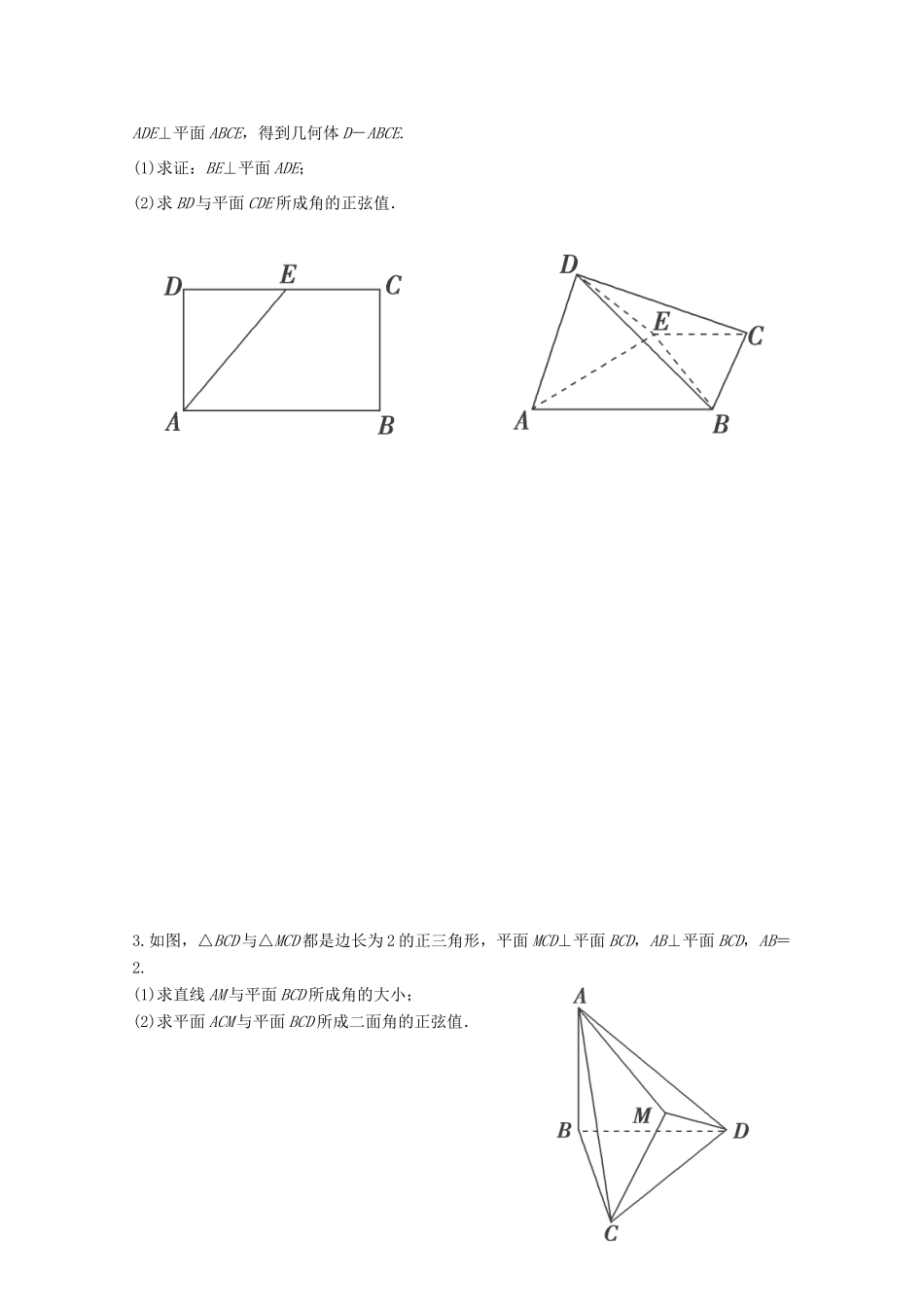
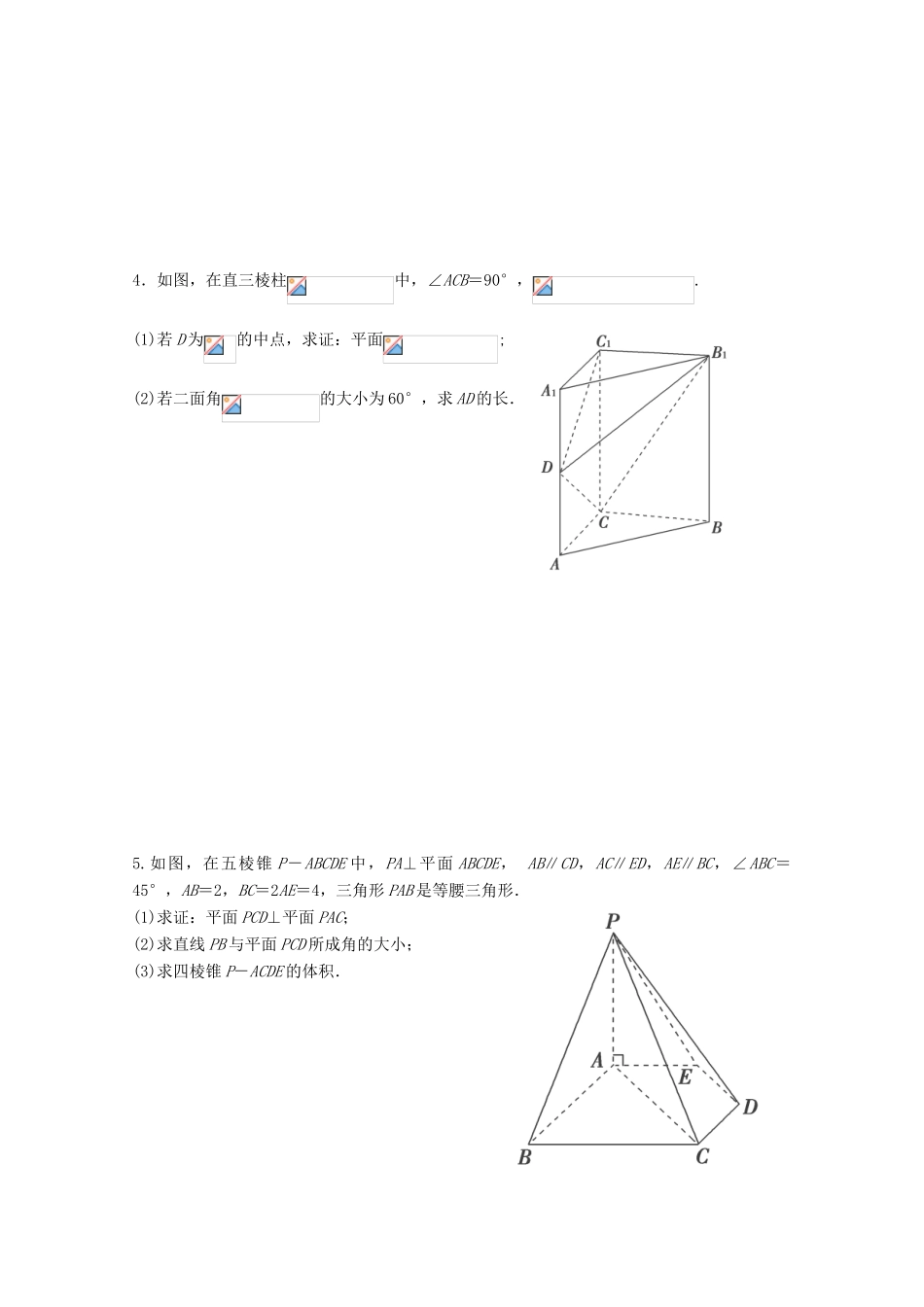
2012 江苏省南京市东山外语国际学校高三数学二轮专题复习《空间向量》导学案(无答案)1.如图所示,在棱长为的正方体中,是 BC 的中点,平面交于点 F.(1)指出 F 在上的位置,并说明理由;(2)求直线与 DE 所成角的余弦值; (3)求直线 AD 与平面所成角的正弦值.2.如图,在矩形 ABCD 中,AB=2,AD=1,E 为 CD 的中点.将△ADE 沿 AE 折起,使平面ADE⊥平面 ABCE,得到几何体 D-ABCE.(1)求证:BE⊥平面 ADE;(2)求 BD 与平面 CDE 所成角的正弦值.3.如图,△BCD 与△MCD 都是边长为 2 的正三角形,平面 MCD⊥平面 BCD,AB⊥平面 BCD,AB=2.(1)求直线 AM 与平面 BCD 所成角的大小;(2)求平面 ACM 与平面 BCD 所成二面角的正弦值. 4.如图,在直三棱柱中,∠ACB=90°,.(1)若 D 为的中点,求证:平面;(2)若二面角的大小为 60°,求 AD 的长. 5.如图,在五棱锥 P-ABCDE 中,PA⊥平面 ABCDE, AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2,BC=2AE=4,三角形 PAB 是等腰三角形.(1)求证:平面 PCD⊥平面 PAC; (2)求直线 PB 与平面 PCD 所成角的大小;(3)求四棱锥 P-ACDE 的体积.