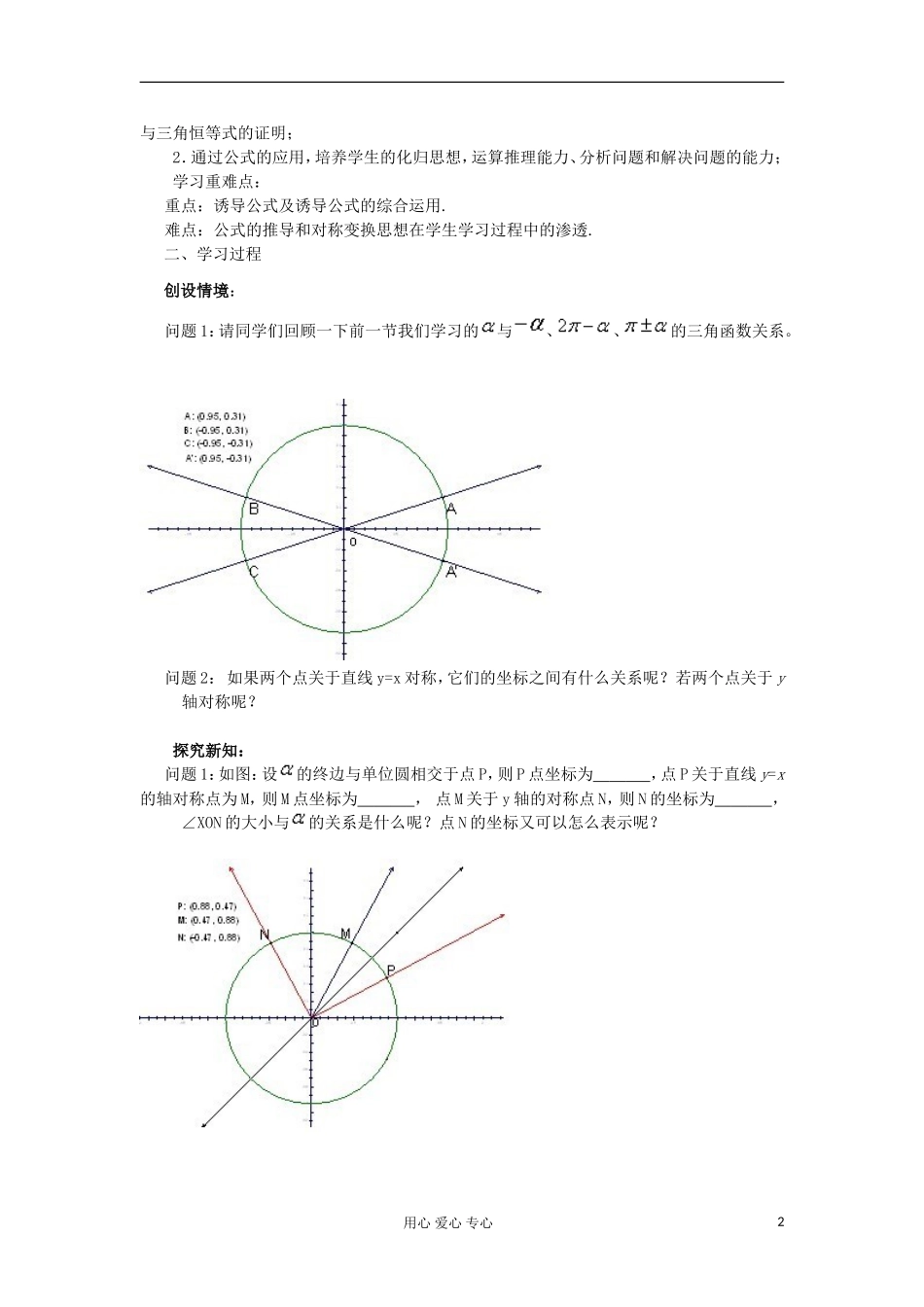
§1.3.2 三角函数诱导公式(二)课前预习学案一、预习目标熟记正弦、余弦和正切的诱导公式,理解公式的由来并能正确地运用这些公式进行任意角的正弦、余弦和正切值的求解、简单三角函数式的化简二、复习与预习1.利用单位圆表示任意角的正弦值和余弦值;____________________2.诱导公式一及其用途: __________________________________________________________________________________________3、对于任何一个内的角,以下四种情况有且只有一种成立(其中为锐角):4、 诱导公式二: 5、诱导公式三:6、诱导公式四: 7、诱导公式五: 8、诱导公式六: 三、提出疑惑同学们,通过你的自主学习,你还有哪些疑惑,请把它填在下面的表格中疑惑点疑惑内容课内探究学案一、学习目标1.通过本节内容的教学,使学生进一步理解和掌握四组正弦、余弦和正切的诱导公式,并能正确地运用这些公式进行任意角的正弦、余弦和正切值的求解、简单三角函数式的化简用心 爱心 专心1与三角恒等式的证明;2.通过公式的应用,培养学生的化归思想,运算推理能力、分析问题和解决问题的能力;学习重难点:重点:诱导公式及诱导公式的综合运用. 难点:公式的推导和对称变换思想在学生学习过程中的渗透.二、学习过程创设情境:问题 1:请同学们回顾一下前一节我们学习的与、、的三角函数关系。 问题 2: 如果两个点关于直线 y=x 对称,它们的坐标之间有什么关系呢?若两个点关于 y轴对称呢? 探究新知:问题 1:如图:设的终边与单位圆相交于点 P,则 P 点坐标为 ,点 P 关于直线 y=x的轴对称点为 M,则 M 点坐标为 , 点 M 关于 y 轴的对称点 N,则 N 的坐标为 , ∠XON 的大小与的关系是什么呢?点 N 的坐标又可以怎么表示呢? 用心 爱心 专心2问题 2:观察点 N 的坐标,你从中发现什么规律了? 例 1 利用上面所学公式求下列各式的值:(1) (2) (3) (4)变式训练 1: 将下列三角函数化为到之间的三角函数:(1) (2) (3)思考:我们学习了的诱导公式,还知道的诱导公式,那么对于,又有怎样的诱导公式呢?例 2 已知方程 sin( 3) = 2cos( 4),求)sin()23sin(2)2cos(5)sin(的值变式训练 2:已知,求的值。课堂练习1.利用上面所学公式求下列各式的值:(1) (2)2.将下列三角函数化为到之间的三角函数:(1) (2)归纳总结:用心 爱心 专...