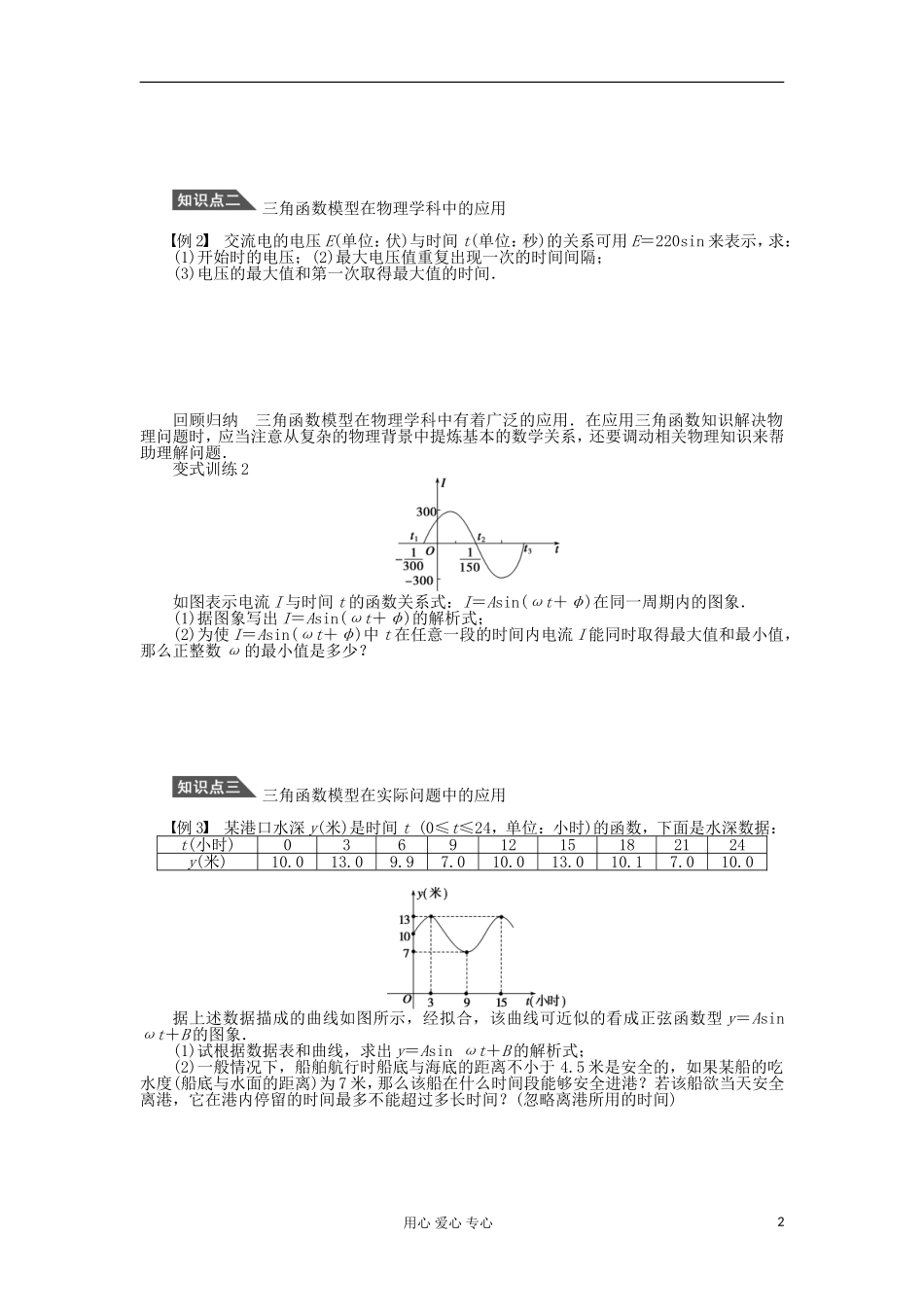
6 三角函数模型的简单应用自主学习1．三角函数的周期性y＝Asin(ωx＋φ) (ω≠0)的周期是 T＝________；y＝Acos(ωx＋φ) (ω≠0)的周期是 T＝________；y＝Atan(ωx＋φ) (ω≠0)的周期是 T＝________
2．函数 y＝Asin(ωx＋φ)＋k (A>0，ω>0)的性质(1)ymax＝________，ymin＝________
(2)A＝__________，k＝__________
(3)ω 可由__________确定，其中周期 T 可观察图象获得．(4)由 ωx1＋φ＝______，ωx2＋φ＝__________，ωx3＋φ＝__________，ωx4＋φ＝__________，ωx5＋φ＝________中的一个确定 φ 的值．3．三角函数模型的应用三角函数作为描述现实世界中________现象的一种数学模型，可以用来研究很多问题，在刻画周期变化规律、预测其未来等方面都发挥着十分重要的作用．结合三角函数图象的特点，思考后写出下列函数的周期．(1)y＝|sin x|的周期是________；(2)y＝|cos x|的周期是________；(3)y＝|tan x|的周期是________；(4)y＝|Asin(ωx＋φ)| (Aω≠0)的周期是________；(5)y＝|Asin(ωx＋φ)＋k| (Aωk≠0)的周期是__________；(6)y＝|Atan(ωx＋φ)| (Aω≠0)的周期是__________．对点讲练从实际问题中提炼三角函数模型例 1 (1)如图(1)所示为一个观览车示意图，该观览车半径为 4
8 m，圆上最低点与地面距离为0
8 m，60 秒转动一圈，图中 OA 与地面垂直，以 OA 为始边，逆时针转动 θ 角到 OB，设 B 点与地面距离为 h
(1)求 h 与 θ 间关系
