2012高中数学 4.2.1《实际问题的函数刻画》精品学案 北师大版必修1

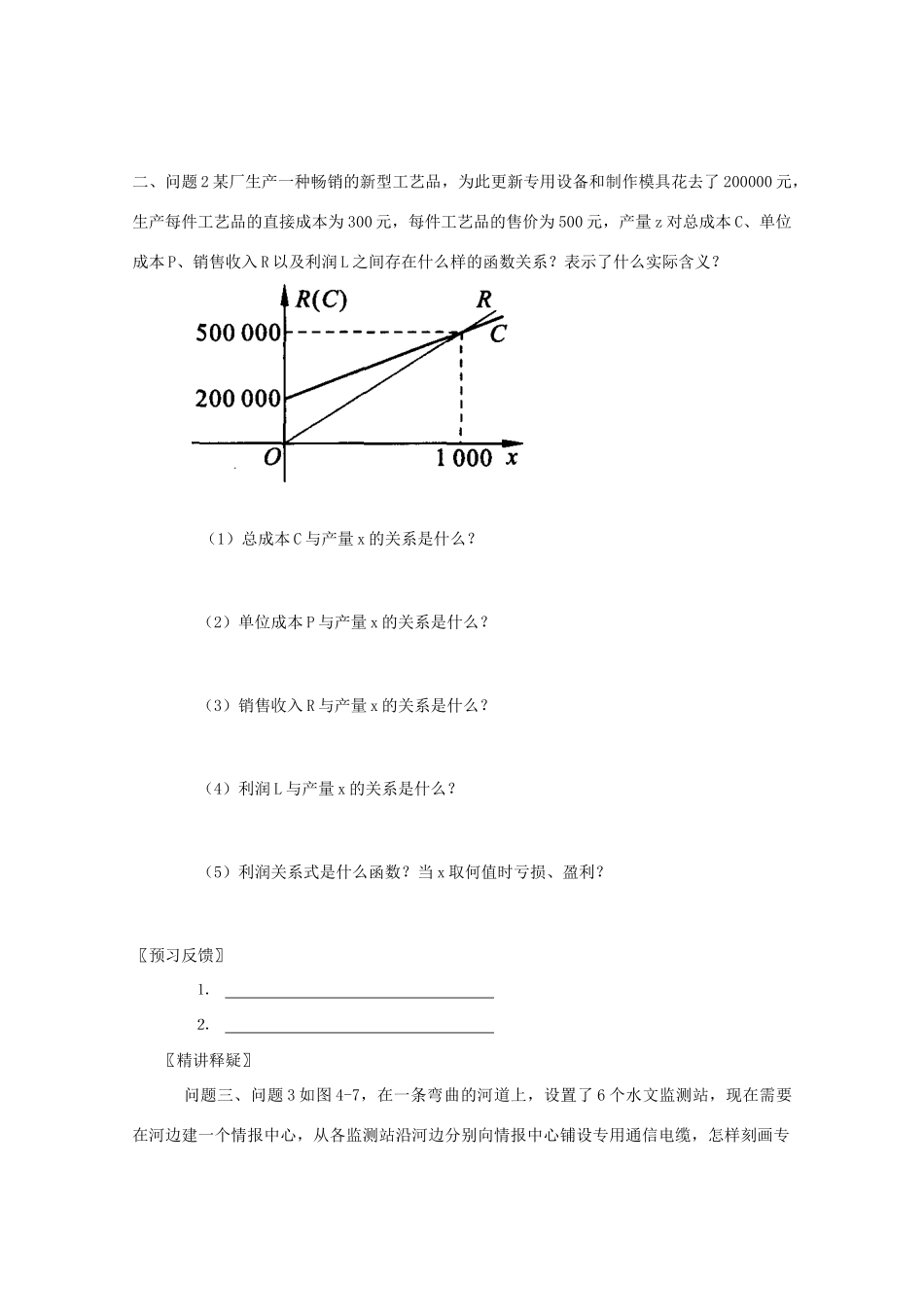
第四章 2.1课题：实际问题的函数刻画【目标要求】〖学习目标〗 1、知道什么叫数学模型，知道数学建模的意义。 2、会用函数刻画现实世界中变量间的依赖关系。 3、知道函数的一些模型。如正反比列函数、一次函数。〖学习重点、难点〗 用函数观点刻画实际问题。（重点） 准确理解题意，理解变量间的关系。（难点）【过程方法】〖预习提要〗一、问题 1 当人的生活环境温度改变时，人体代谢率也有相应的变化，表 4-2 给出了实验的一组数据，这组数据能说明什么？ 环境温度／(℃) 4 10 20 30 38 代谢率/[4185J/(h .m2)] 60 44 40 40.5 54（⒈）在这个实际问题中出现了几个变量？它们之间能确定函数关系吗？为什么？（2）、结合图 4-5 分析代谢率在什么范围下降，什么范围上升？ （3）温度在什么范围内代谢率变化较小比较稳定，什么范围代谢率变化较大？二、问题 2 某厂生产一种畅销的新型工艺品，为此更新专用设备和制作模具花去了 200000 元，生产每件工艺品的直接成本为 300 元，每件工艺品的售价为 500 元，产量 z 对总成本 C、单位成本 P、销售收入 R 以及利润 L 之间存在什么样的函数关系？表示了什么实际含义？ （1）总成本 C 与产量 x 的关系是什么？（2）单位成本 P 与产量 x 的关系是什么？（3）销售收入 R 与产量 x 的关系是什么？（4）利润 L 与产量 x 的关系是什么？（5）利润关系式是什么函数？当 x 取何值时亏损、盈利？〖预习反馈〗⒈ ⒉ 〖精讲释疑〗 问题三、问题 3 如图 4-7，在一条弯曲的河道上，设置了 6 个水文监测站，现在需要在河边建一个情报中心，从各监测站沿河边分别向情报中心铺设专用通信电缆，怎样刻画专用通信电缆的总长度？〖检测拓展〗类型一：数学模型为正比列、反比列函数的问题1、 一个圆柱形容器的底面直径为 dcm,高度为 hcm，现以每秒 S的速度向容器内注入某种溶液，求容器内溶液高度 y 与时间 t（秒）的函数关系式及定义域。2、有 m 部同样的机器一起工作，需要 m 小时完成一项任务。（1）设由 x 部机器（x 为不大于 m 的正整数）完成同一任务，求所需时间 y（小时）与机器的部数 x 的函数关系式。（2）画出所求函数当 m=4 时的图像。类型二：数学模型为一次函数2、 某家报刊销售店从报社买进报纸的价格是每份 0.35 元，卖出的价格是每份 0.50 元，卖不掉的报纸还可以以每份 0.08 元的价格退回报社。在一个月...