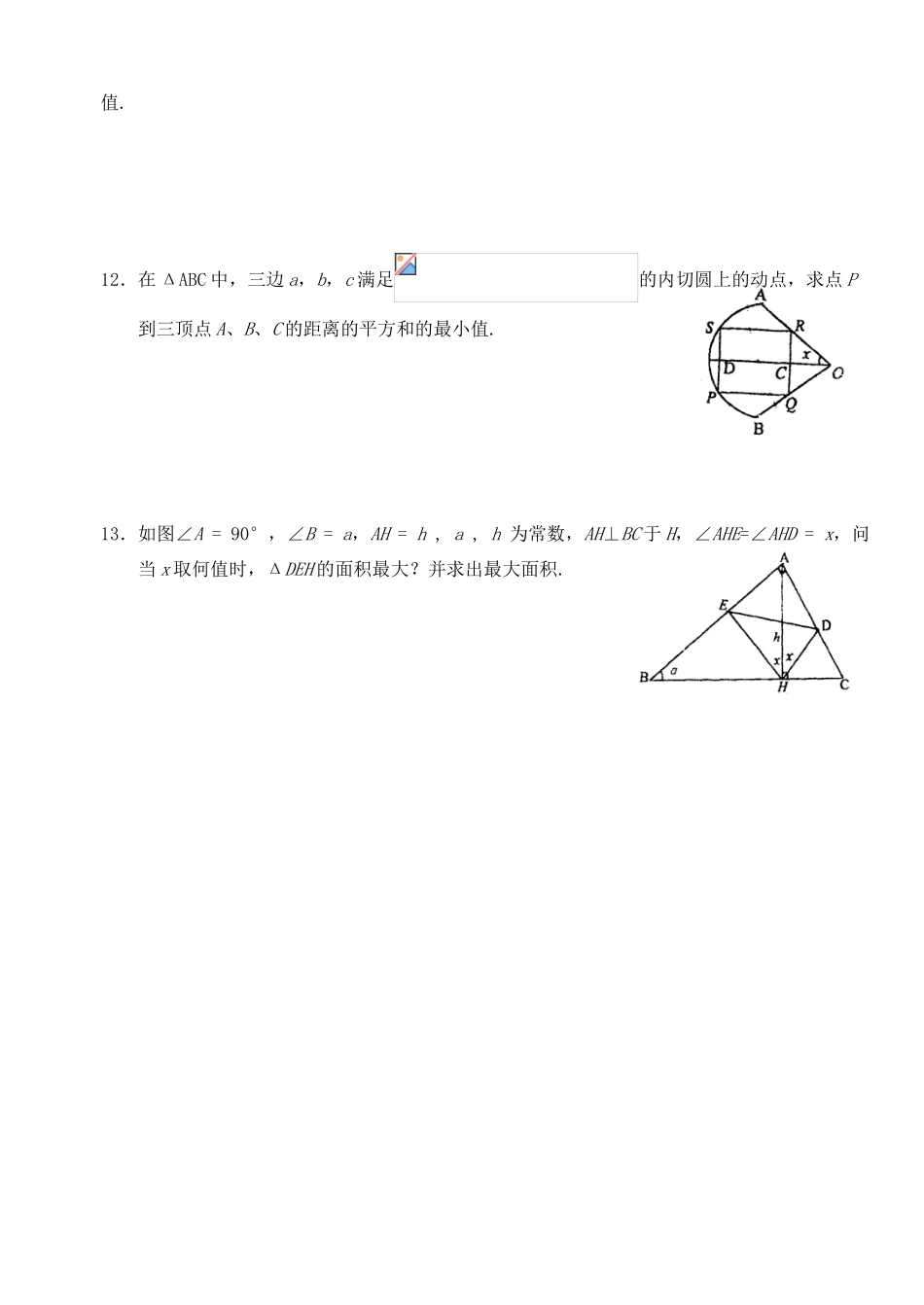
3.14 三角最值问题1.求三角函数最值的方法: ① 利用三角函数的有界性; ② 转化为二次函数; ③ 利用平均值定值; ④ 利用判别式法; ⑤ 利用函数的单调性; ⑥ 利用换元法.2.三角函数的最值问题中对参数讨论的方法.3.隐含条件在最值问题中讨论.【典型例题】例 1.求函数的最大值和最小值.例 2.在内切圆半径为 r(定值)的直角三角形中,试证明等腰三角形的周长为最短.例 3.已知抛物线 y = x2-xcosθ+ 2sinθ-1(θ 为参数), (1)求此抛物线在 x 轴上两截距的平方和与 θ 的函数关系 f(θ);(2)求 f(θ)的最小值和最大值.例 4.已知 ΔABC 的三边 a、b、c 和面积 S 满足关系式 S = a2-(b-c)2,且 b + c = 8,求ΔABC面积最大值.【基础训练】1.函数上的最小值是______________.2.x =_________时,函数的最大值为_____________.3.已知 2α+β=π,求 y = cosβ-6sinα 的最大值_____________,最小值是_____________.4.函数 f(x) = sinx + cosx 在区间[0,π]上的最大值是____________,最小值是__________.5.已知 x2 + y2 = 4,求 A = x2 + xy + y2的最大值和最小值.【拓展练习】1.在 ΔABC 中,∠C=,则 sin2A + 2sinB( )A.有最大值无最小值B.有最小值无最大值C.有最大值也有最小值D.无最小值也无最大值2.RtΔ 斜边的长 C(定值),则它的周长的最大值是( )A.B.2CC.D.3C3.,则( )A.最小值为-2,最大值为 0B.最小值为-4,最大值为 0C.无最小值,最大值为 0D.最小值为-4,最大值为 04.函数的最大值是________________.5.设 R,r 分别为 RtΔ 的外接圆半径和内切圆半径,则的最大值为_____________.6.已知 ΔABC 中,A = 30°,BC = 4,则 AB + AC 的最大值为_____________.7.函数的最大值是_____________.8.已知 0≤x<2π,a 为实常数,求函数的最大值.9.求函数 y = (1 + cosx ) sinx 在区间[0,π]内的最大值.10.在 ΔABC 中,若∠A 和 ΔABC 的面积 S 为定值,求当 2a2 + 3c2取得最小值时,b : c 之值.11.设 tanα,tanβ 是关于 x 的方程的两个实根,求 tan (α+β)最小值.12.在 ΔABC 中,三边 a,b,c 满足的内切圆上的动点,求点 P到三顶点 A、B、C 的距离的平方和的最小值.13.如图∠A = 90°,∠B = a,AH = h , a , h 为常数,AH⊥BC 于 H,∠AHE=∠AHD = x,问当 x 取何值时,ΔDEH 的面积最大?并求出最大面积.