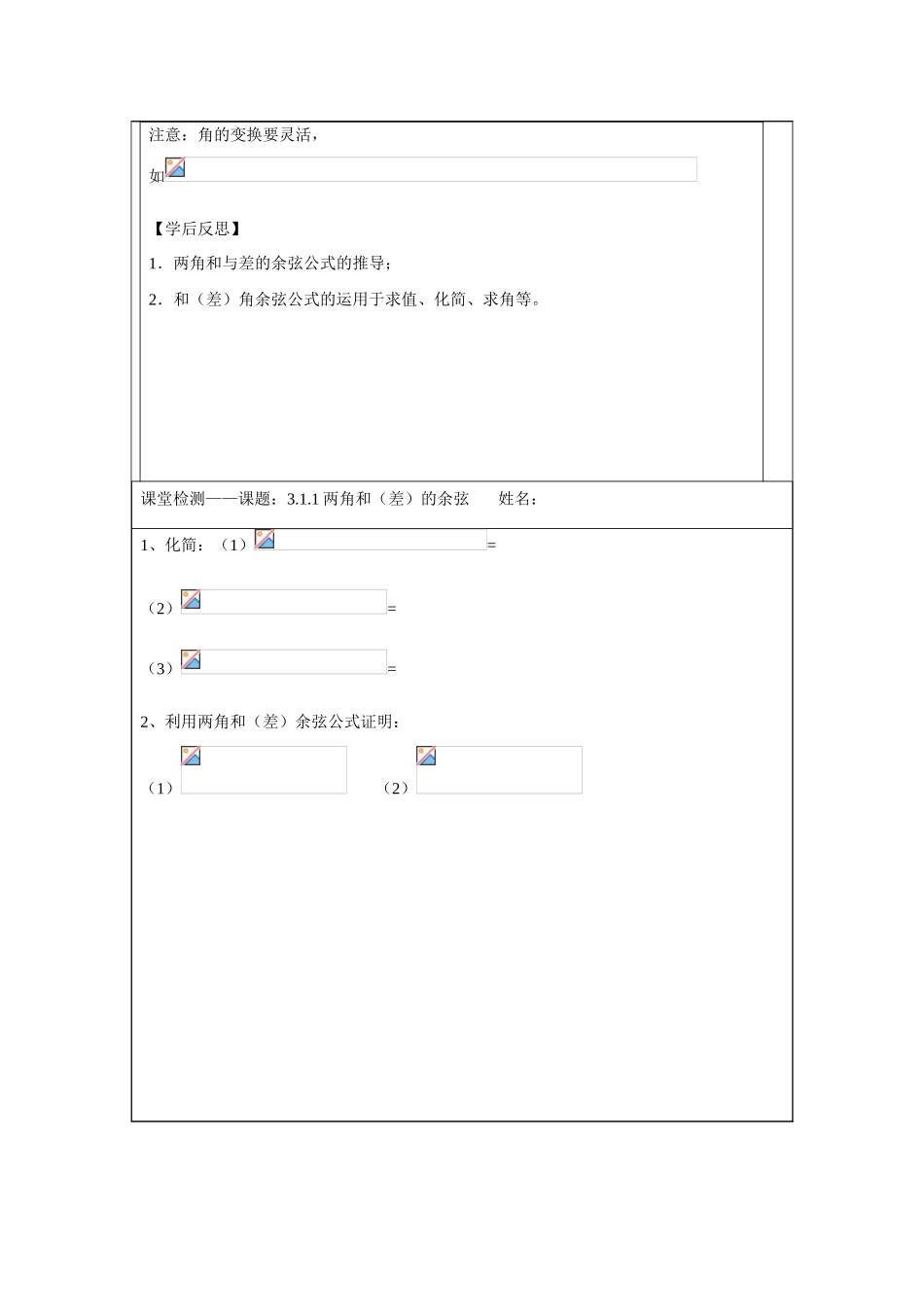
课题:3.1.1 两角和与差的余弦班级: 姓名: 学号: 第 学习小组【学习目标】1.会用向量的数量积推导两角差的余弦公式,体会向量与三角函数之间的关系;2.能用和差角的余弦公式进行简单的三角函数式的化简、求值、证明【课前预习】1.已知向量,夹角为,则= = 2.由两向量的数量积研究两角差的余弦公式= ,简记作:3.在上述公式中,用代替得两角和的余弦公式:= ,简记作:【课堂研讨】例 1.利用两角和(差)余弦公式证明下列诱导公式: 例 2、利用两角和(差)的余弦公式,求的值。例 3、已知,求的值。变式:在例 3 中,你能求的值吗?例 4.若,求注意:角的变换要灵活,如【学后反思】1.两角和与差的余弦公式的推导;2.和(差)角余弦公式的运用于求值、化简、求角等。课堂检测——课题:3.1.1 两角和(差)的余弦 姓名:1、化简:(1)= (2)= (3)= 2、利用两角和(差)余弦公式证明:(1) (2)3、已知求的值课外作业 班级:高一( )班 姓名__________1、= 2、在中,已知,则的形状为 3、计算(1) (2)= 4、化简:(1)= (2) 5、已知都是锐角,,则= 6、已知= 7、(1)已知;(2)已知。8、已知,求的值。课题:3.1.1 两角和与差的余弦班级: 姓名: 学号: 第 学习小组【学习目标】1.会用向量的数量积推导两角差的余弦公式,体会向量与三角函数之间的关系;2.能用和差角的余弦公式进行简单的三角函数式的化简、求值、证明【课前预习】1.已知向量,夹角为,则= = 2.由两向量的数量积研究两角差的余弦公式= ,简记作:3.在上述公式中,用代替得两角和的余弦公式:= ,简记作:【课堂研讨】例 1.利用两角和(差)余弦公式证明下列诱导公式: 例 2、利用两角和(差)的余弦公式,求的值。例 3、已知,求的值。变式:在例 3 中,你能求的值吗?例 4.若,求注意:角的变换要灵活,如【学后反思】1.两角和与差的余弦公式的推导;2.和(差)角余弦公式的运用于求值、化简、求角等。课堂检测——课题:3.1.1 两角和(差)的余弦 姓名:1、化简:(1)= (2)= (3)= 2、利用两角和(差)余弦公式证明:(1) (2)3、已知求的值课外作业 班级:高一( )班 姓名__________1、= 2、在中,已知,则的形状为 3、计算(1) (2)= 4、化简:(1)= (2) 5、已知都是锐角,,则= 6、已知= 7、(1)已知;(2)已知。8、已知,求的值。