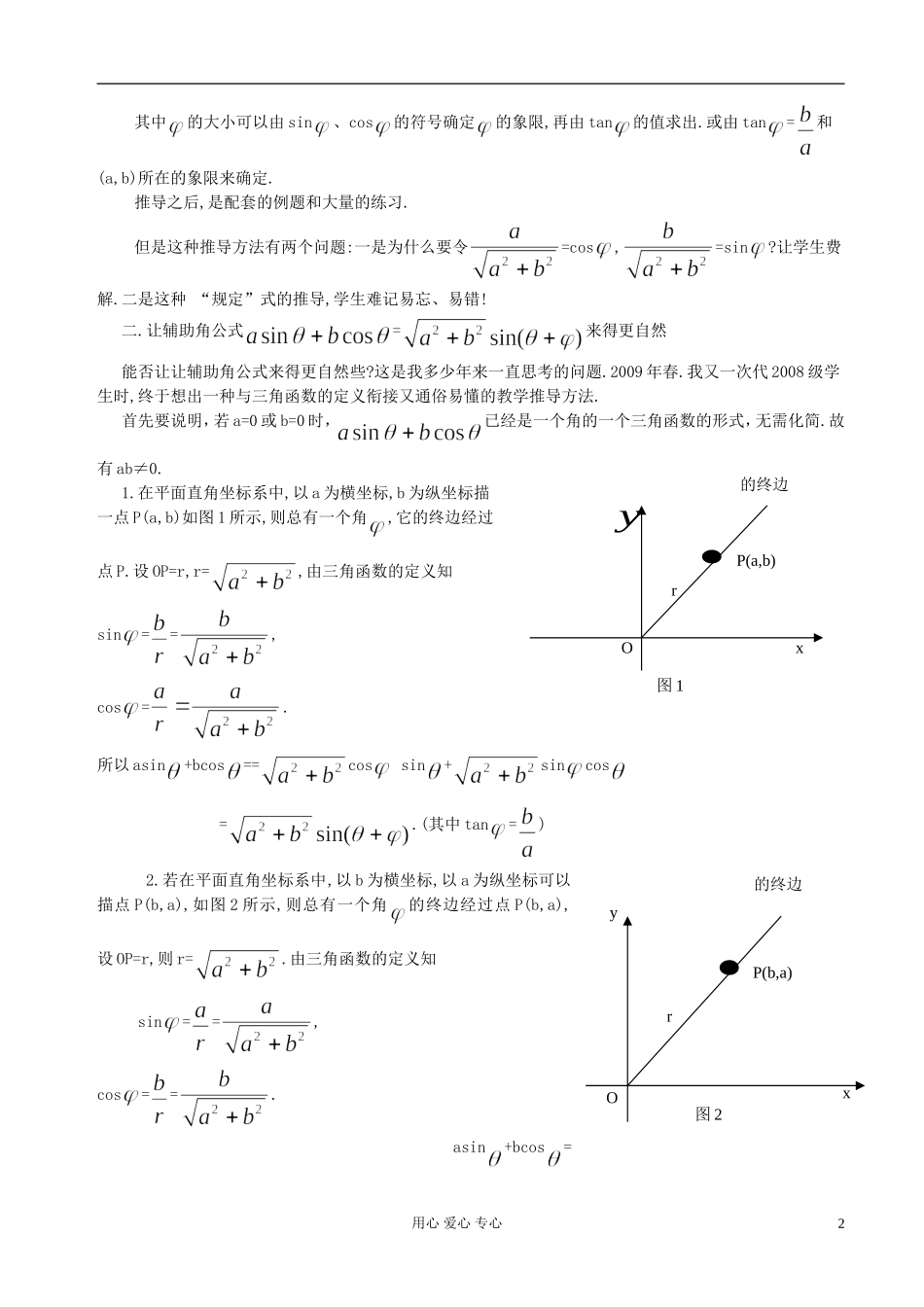
辅助角公式教学 在三角函数中,有一种常见而重要的题型,即化为一个角的一个三角函数的形式,进而求原函数的周期、值域、单调区间等.为了帮助学生记忆和掌握这种题型的解答方法,教师们总结出公式=或=·,让学生在大量的训练和考试中加以记忆和活用.但事与愿违,半个学期不到,大部分学生都忘了,教师不得不重推一遍.到了高三一轮复习,再次忘记,教师还得重推!本文旨在通过辅助角公式的另一种自然的推导,体现一种解决问题的过程与方法,减轻学生的记忆负担;同时说明“辅助角”的范围和常见的取角方法,帮助学生澄清一些认识;另外通过例子说明辅助角公式的灵活应用,优化解题过程与方法;最后通过例子说明辅助公式在实际中的应用,让学生把握辅助角与原生角的范围关系,以更好地掌握和使用公式.一.教学中常见的的推导方法教学中常见的推导过程与方法如下1.引例例 1 求证:sin+cos=2sin(+)=2cos(-).其证法是从右往左展开证明,也可以从左往右“凑”,使等式得到证明,并得出结论:可见, sin+cos可以化为一个角的三角函数形式. 一般地,asin+bcos 是否可以化为一个角的三角函数形式呢? 2.辅助角公式的推导例 2 化为一个角的一个三角函数的形式. 解: asin+bcos=(sin+cos),① 令=cos,=sin,则 asin+bcos=(sincos+cossin)=sin(+),(其中 tan=)② 令=sin,=cos,则 asin+bcos=(sinsin+coscos)=cos(-),(其中 tan=)用心 爱心 专心1其中的大小可以由 sin、cos的符号确定的象限,再由 tan的值求出.或由 tan=和(a,b)所在的象限来确定.推导之后,是配套的例题和大量的练习.但是这种推导方法有两个问题:一是为什么要令=cos,=sin?让学生费解.二是这种 “规定”式的推导,学生难记易忘、易错!二.让辅助角公式=来得更自然能否让让辅助角公式来得更自然些?这是我多少年来一直思考的问题.2009 年春.我又一次代 2008 级学生时,终于想出一种与三角函数的定义衔接又通俗易懂的教学推导方法.首先要说明,若 a=0 或 b=0 时,已经是一个角的一个三角函数的形式,无需化简.故有 ab≠0.1.在平面直角坐标系中,以 a 为横坐标,b 为纵坐标描一点 P(a,b)如图 1 所示,则总有一个角,它的终边经过点 P.设 OP=r,r=,由三角函数的定义知sin==,cos=.所以 asin+bcos==cos sin+sincos =.(其中 tan=)2.若在平面直角坐标系中,以 b 为横坐标,以 a 为纵坐标可以描点 P(b,a),如图 2 所示,则总有一个角的终边经过点 P(b,a),设 OP=r,则 r=.由三角函数的定义知 sin...