2013-2014学年高中数学 三角函数线教案 新人教A版必修1

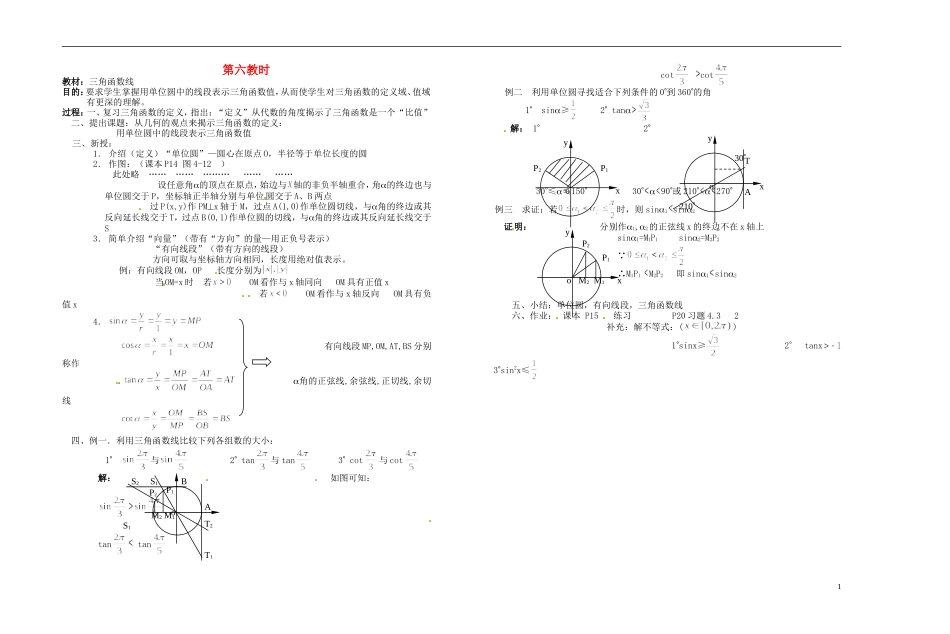
第六教时教材：三角函数线目的：要求学生掌握用单位圆中的线段表示三角函数值，从而使学生对三角函数的定义域、值域有更深的理解。过程：一、复习三角函数的定义，指出：“定义”从代数的角度揭示了三角函数是一个“比值”二、提出课题：从几何的观点来揭示三角函数的定义：用单位圆中的线段表示三角函数值三、新授：1． 介绍（定义）“单位圆”—圆心在原点 O，半径等于单位长度的圆2． 作图：（课本 P14 图 4-12 ）此处略 …… …… ……… …… …… 设任意角的顶点在原点，始边与 轴的非负半轴重合，角的终边也与单位圆交于 P，坐标轴正半轴分别与单位圆交于 A、B 两点 过 P(x,y)作 PMx 轴于 M，过点 A(1,0)作单位圆切线，与角的终边或其反向延长线交于 T，过点 B(0,1)作单位圆的切线，与角的终边或其反向延长线交于S3． 简单介绍“向量”（带有“方向”的量—用正负号表示）“有向线段”（带有方向的线段）方向可取与坐标轴方向相同，长度用绝对值表示。例：有向线段 OM，OP 长度分别为 当OM=x 时 若 OM 看作与 x 轴同向 OM 具有正值 x 若 OM 看作与 x 轴反向 OM 具有负值 x4． 有向线段 MP,OM,AT,BS 分别称作 角的正弦线,余弦线,正切线,余切线 四、例一．利用三角函数线比较下列各组数的大小：1 与 2 tan与 tan 3 cot与 cot 解： 如图可知： tan tan cot cot 例二 利用单位圆寻找适合下列条件的 0到 360的角1 sin≥ 2 tan 解： 1 2 30≤≤150 30  90或 210  270例三 求证：若时，则 sin1 sin2证明： 分别作1,2的正弦线 x 的终边不在 x 轴上 sin1=M1P1 sin2=M2P2 ∵∴M1P1 M2P2 即 sin1 sin2五、小结：单位圆，有向线段，三角函数线六、作业： 课本 P15 练习 P20 习题 4.3 2 补充：解不等式：() 1sinx≥ 2 tanx 3sin2x≤1ABoT2T1 S2 S1P2P1 M2 M1 S1xyoP1P2xyoTA21030xyoP1P2M1M2