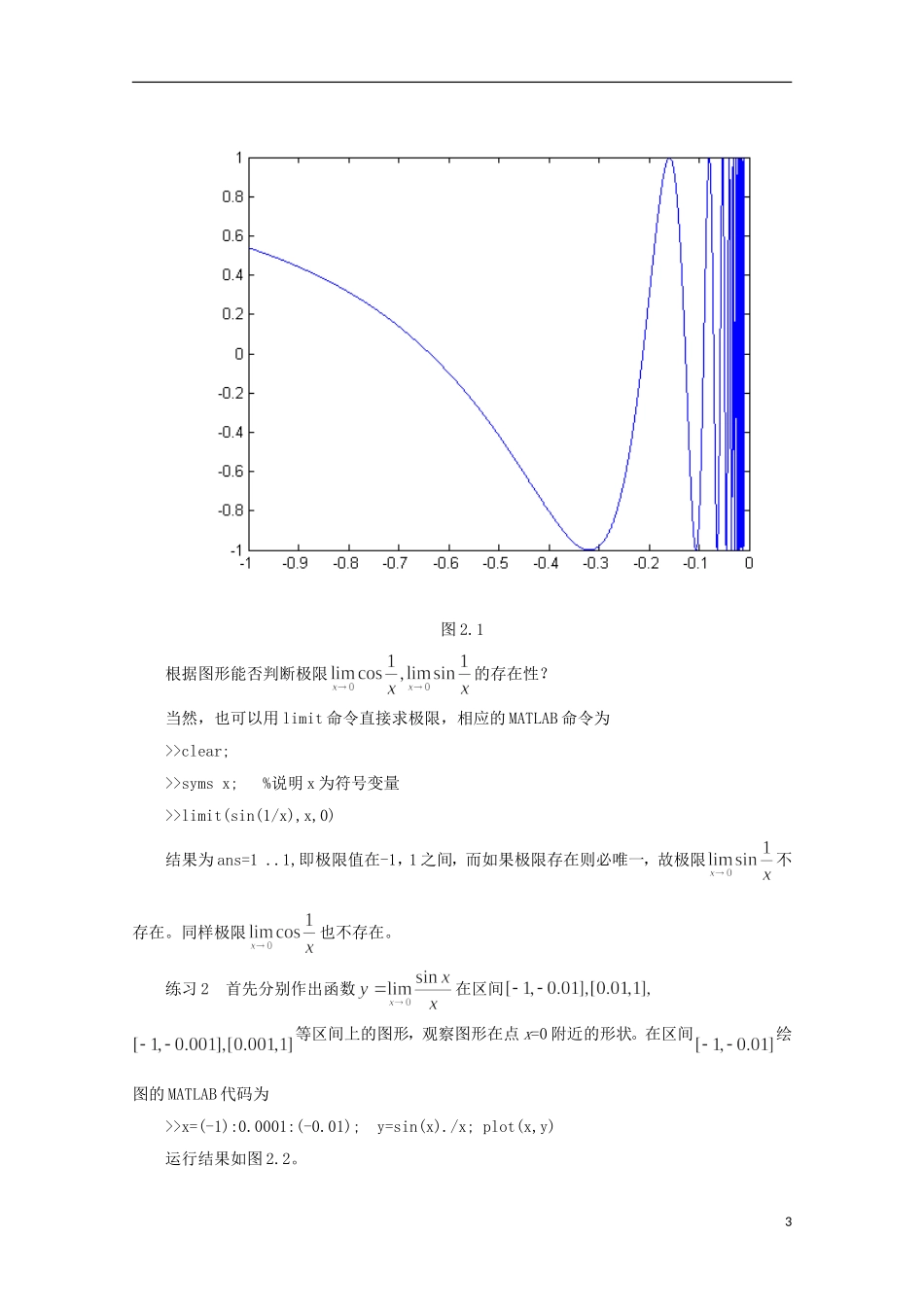
2013 年高中数学 1.2 1 极限与导数教案 新人教 A 版选修 2-2【实验目的】1.了解函数极限、导数的基本概念。2.学习、掌握 MATLAB 软件有关求曲线、导数的命令。【实验内容】1.判断极限的存在性。2.验证极限。3.验证极限。4.求函数的单调区间及极值。【实验准备】1.极限导数的基本概念2.求极限、导数的 MATLAB 命令MATLAB 主要用 limit,diff 分别求函数的极限与导数。建立符号变量命令 sym 和 syms 调用格式: x=sym('x'), 建立符号变量 x; syms x y z , 建立多个符号变量 x,y,z; matlab 求导命令 diff 调用格式: diff(函数) , 求的一阶导数; diff(函数, n) , 求的 n 阶导数(n 是具体整数); diff(函数,变量名 ), 求对 的偏导数; diff(函数, 变量名 ,n) ,求对 的 n 阶偏导数;1matlab求雅可比矩阵命令 jacobian,调用格式: jacobian([函数;函数; 函数], [])给出矩阵: 【实验重点】1.极限的计算2.导数的计算【实验难点】1.导数的曲线表示【实验方法与步骤】一、观察与练习练习 1 首先分别作出函数在区间等区间上的图形,观察图形在附近的形状。在区间绘图的 MATLAB 代码为>>x=(-1):0.0001:(-0.01); y=cos(1./x);plot(x,y)运行结果如图 2.1。2图 2.1根据图形能否判断极限的存在性?当然,也可以用 limit 命令直接求极限,相应的 MATLAB 命令为>>clear;>>syms x; %说明 x 为符号变量>>limit(sin(1/x),x,0)结果为 ans=1 ..1,即极限值在-1,1 之间,而如果极限存在则必唯一,故极限不存在。同样极限也不存在。练习 2 首先分别作出函数在区间等区间上的图形,观察图形在点 x=0 附近的形状。在区间绘图的 MATLAB 代码为>>x=(-1):0.0001:(-0.01); y=sin(x)./x; plot(x,y)运行结果如图 2.2。3图 2.2根据图形,能否判断极限的正确性?当然,也可以用 limit 命令直接求极限,相应的 MATLAB 命令为>>clear;>>syms x; >>limit(sin(x)/x),x,0)结果为 ans=1。二、极限计算例 2.1.观察数列当时的变化趋势.解:输入命令: n=1:100;xn=n./(n+1)得到该数列的前 100 项,从这前 100 项看出,随 的增大,与 1 非常接近,画出的图形.4 stem(n,xn)或 for i=1:100; plot(n(i),xn(i),’r’) hold on end其中 for … end 语句是循环语句,循环体内的语句被执行 100 次,n(i)表示 n 的第 i 个分量.由图可看出,随 的增大,点列与直...