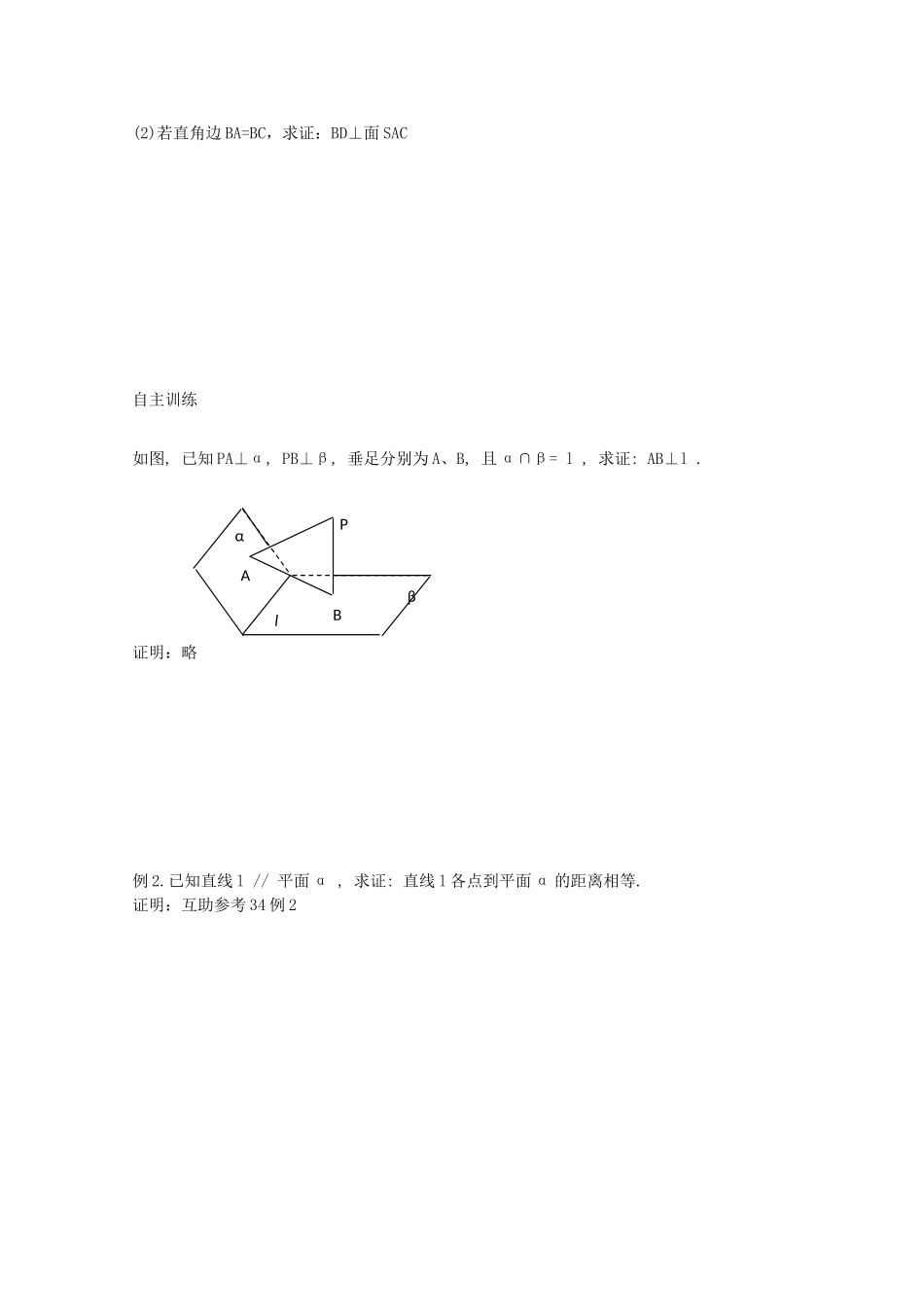
第 10 课时 直线与平面垂直 一、【学习导航】知识网络学习要求 1.掌握直线与平面的位置关系.2.掌握直线和平面平行的判定与性质定理..3.应用直线和平面平行的判定和性质定理证明两条直线平行等有关问题.【课堂互动】自学评价1. 直线和平面垂直的定义: 符号表示: 垂线: 垂面: 垂足: 思考:在平面中,过一点有且仅有一条直线与已知直线垂直,那么在空间。(1)过一点有几条直线与已知平面垂直?答:(2)过一点有几条平面与已知直线垂直?答:2.定理:过一点有且只有一条直线与已知平面垂直,过一点有且只有一个平面与已知直线垂直3.点到平面的距离: 直线和平面垂直的定义直线和平面垂直直线和平面垂直的判定直线和平面垂直的判定与性质定理的应用直线和平面垂直的性质4.直线与平面垂直的判定定理: 符号表示 5.直线和平面垂直的性质定理: 已知:求证:证明:互助参考 346.直线和平面的距离: 【精典范例】例 1:.求证: 如果两条平行直线中的一条垂直于一个平面, 那么另一条直线也垂直于这个平面.证明:互助参考 34 例 1思维点拔:要证线面垂直,只要证明直线与平面内的两条相交直线垂直,或利用定义进行证明。Rt△ABC 所在平面外一点S,且 SA=SB=SC(1)求证:点S在斜边中点D的连线 SD⊥面 ABC(2)若直角边 BA=BC,求证:BD⊥面 SAC自主训练如图, 已知 PA⊥α, PB⊥β, 垂足分别为 A、B, 且 α∩β= l , 求证: AB⊥l .证明:略例 2.已知直线 l // 平面 α , 求证: 直线 l 各点到平面 α 的距离相等.证明:互助参考 34 例 2ABPαβl例 3.已知正方体 ABCD-A1B1C1D1 .(1)求证: A1C⊥B1D1 ; (2)若 M、N 分别为 B1D1与 C1D 上的点, 且 MN⊥B1D1 , MN⊥C1D , 求证: MN//A1C .分析:(1)可先证 B1D1⊥面 A1CC1,从而证出结论.(2)可证 MN 和 A1C 都垂直于面 BDC1, 从而利用性质证出结论点评:要证线线平行均可利用线面垂直的性质。自主训练1.已知直线 l,m,n 与平面 α,指出下列命题是否正确,并说明理由:(1)若 l⊥α,则 l 与 α 相交;(2)若 mα,nα,l⊥m,l⊥n,则 l⊥α;(3)若 l//m,m⊥α,n⊥α,则 l//m 2.某空间图形的三视图如图所示,试画出它的直观图,并指出其中的线面垂直关系.ABDCD1=C1=B1=A1=M=N3.在△ABC 中,∠B=90°,SA⊥面 ABC,AM⊥SC,AN⊥SB 垂足分别为 N、M,求证:AN⊥BC,MN⊥SC略证:BC⊥面 SABBC⊥AN再证 AN⊥面 SBC AN⊥SC AM⊥SC SC⊥面 ANM MN⊥SC BANMCS