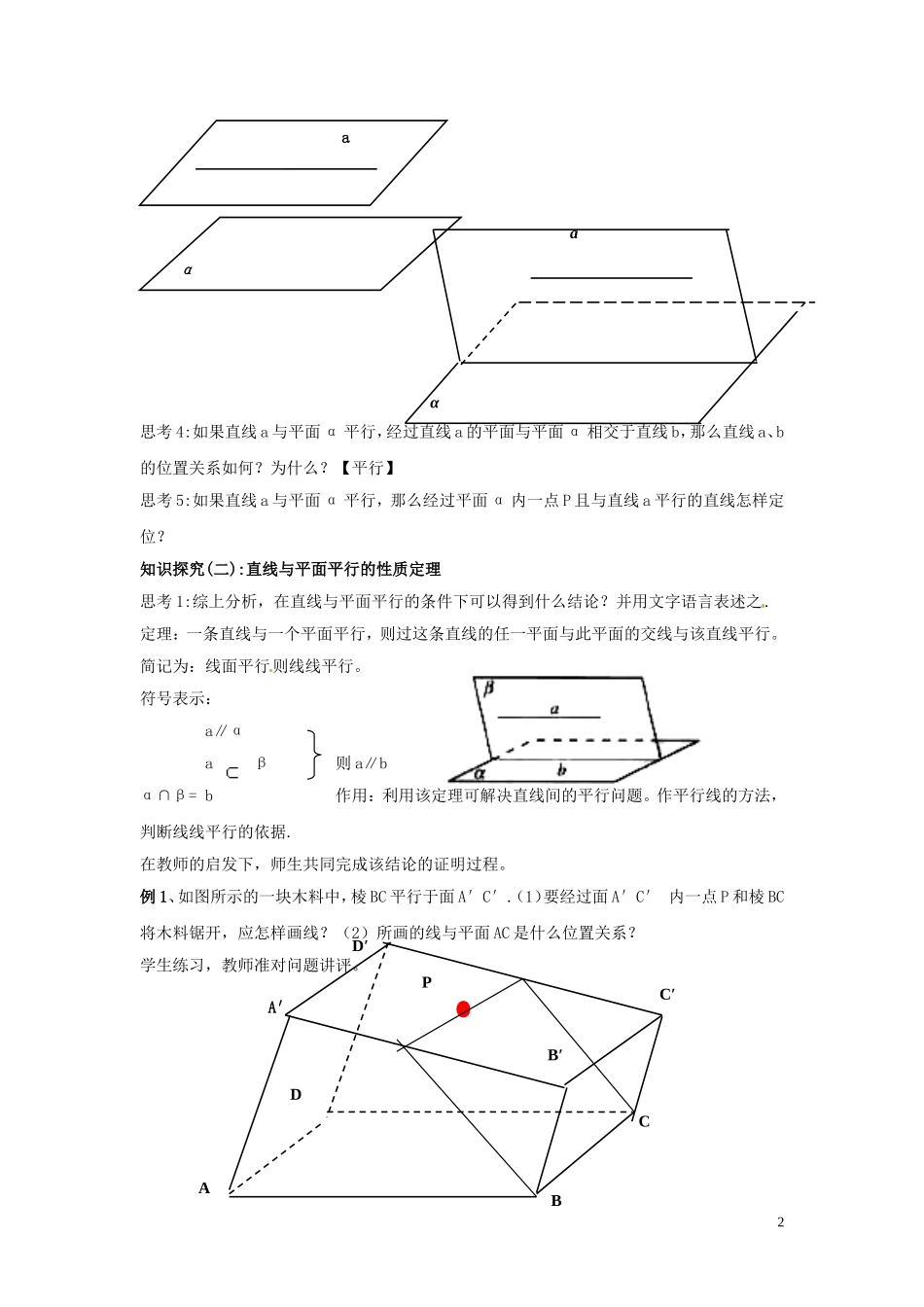
第十一课时§2.2.3 — 2.2.4 直线与平面、平面与平面平行的性质一、教学目标1、知识与技能:(1)掌握直线与平面平行的性质定理及其应用;(2)掌握两个平面平行的性质定理及其应用。2、过程与方法:学生通过观察与类比,借助实物模型理解性质及应用。3、情感、态度与价值观:(1)进一步提高学生空间想象能力、思维能力;(2)进一步体会类比的作用;(3)进一步渗透等价转化的思想。二、教学重点、难点:重点:两个性质定理 。难点:(1)性质定理的证明;(2)性质定理的正确运用。三、学法与教法1、学法:学生借助实物,通过类比、交流等,得出性质及基本应用。2、教法:探究讨论法四、教学过程(一)、创设情景、引入新课思考题:教材第 60 页,思考(1)(2)。学生思考、交流,得出(1)一条直线与平面平行,并不能保证这个平面内的所有直线都与这个直线平行;(2)直线a 与平面 α 平行,过直线 a 的某一平面,若与平面 α 相交,则直线 a 就平行于这条交线。(二)、探究新知知识探究(一):直线与平面平行的性质分析 思考 1:如果直线 a 与平面 α 平行,那么直线 a 与平面 α 内的直线有哪些位置关系?思考 2:若直线 a 与平面 α 平行,那么在平面 α 内与直线 a 平行的直线有多少条?这些直线的位置关系如何?思考 3:如果直线 a 与平面 α 平行,那么经过直线 a 的平面与平面 α有几种位置关系?aα1aα思考 4:如果直线 a 与平面 α 平行,经过直线 a 的平面与平面 α 相交于直线 b,那么直线 a、b的位置关系如何?为什么?【平行】思考 5:如果直线 a 与平面 α 平行,那么经过平面 α 内一点 P 且与直线 a 平行的直线怎样定位?知识探究(二):直线与平面平行的性质定理 思考 1:综上分析,在直线与平面平行的条件下可以得到什么结论?并用文字语言表述之.定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。简记为:线面平行则线线平行。符号表示:a∥αa β 则 a∥bα∩β= b 作用:利用该定理可解决直线间的平行问题。作平行线的方法,判断线线平行的依据. 在教师的启发下,师生共同完成该结论的证明过程。例 1、如图所示的一块木料中,棱 BC 平行于面 A′C′.(1)要经过面 A′C′ 内一点 P 和棱 BC将木料锯开,应怎样画线?(2)所画的线与平面 AC 是什么位置关系? 学生练习,教师准对问题讲评。αa2AA′CBDPD...