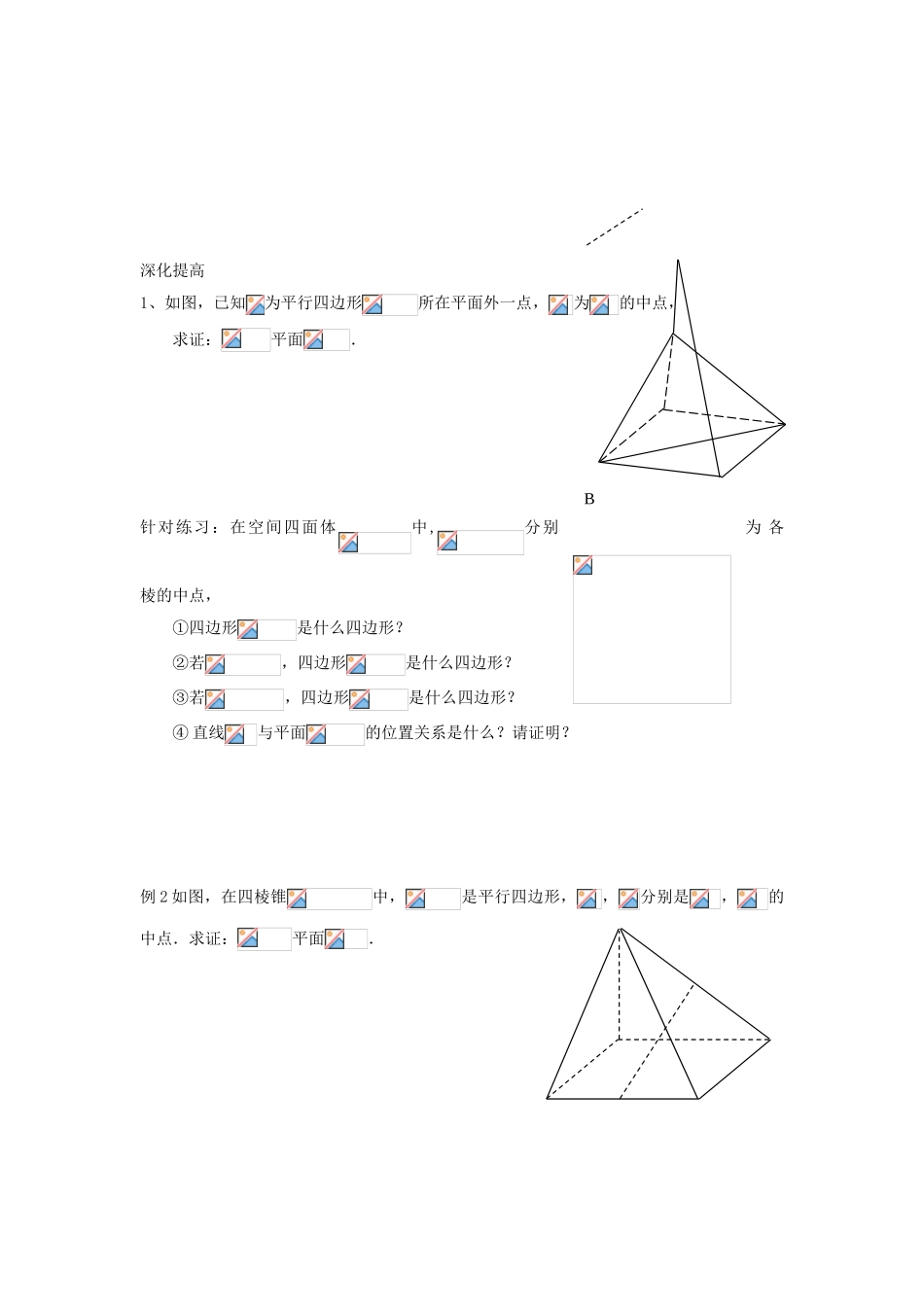
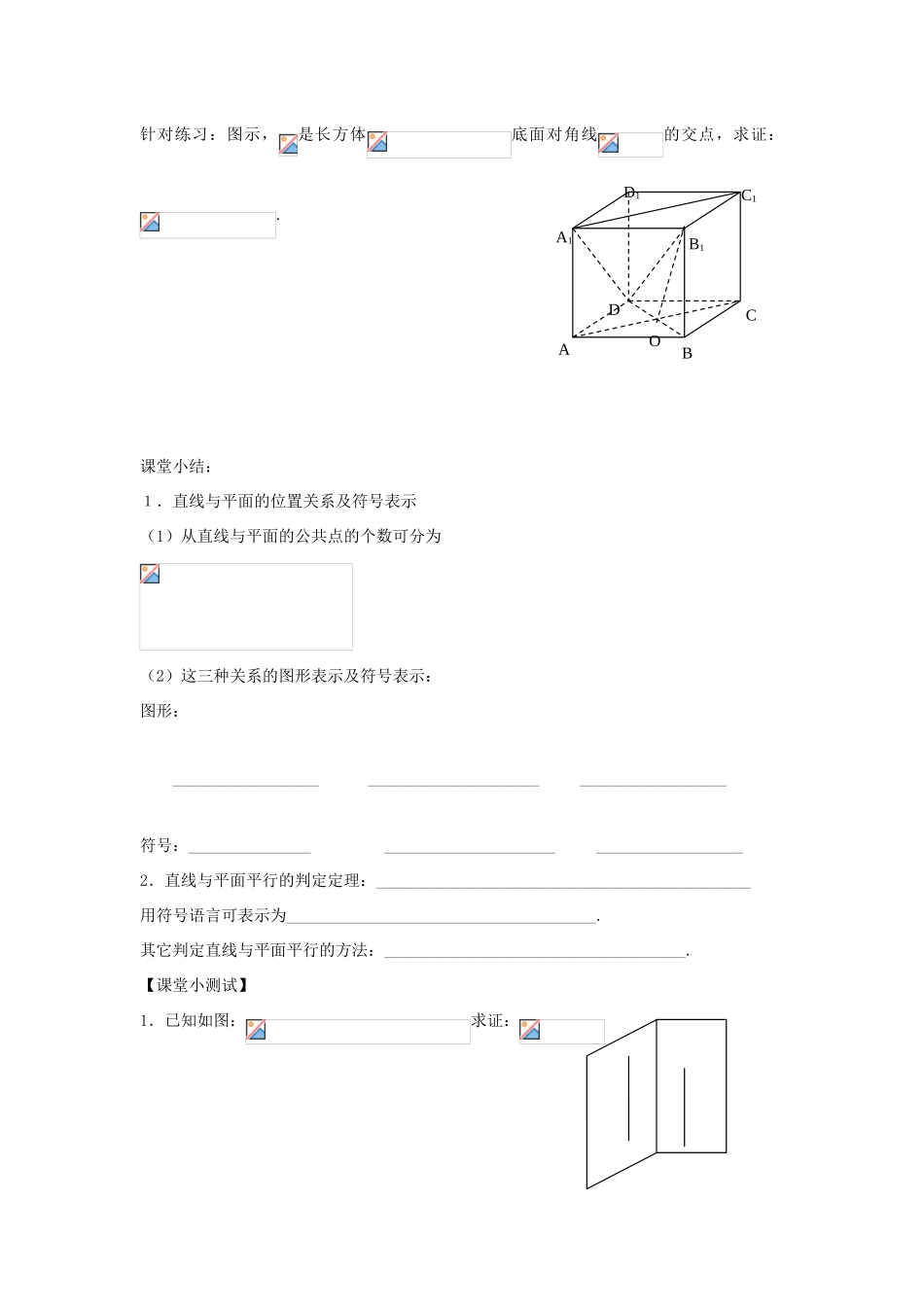
2014 年高中数学 2.2 直线与平面平行学案 新人教 A 版必修 2学习目标:(1)让学生通过实例操作,认识直线和平面的位置关系,并能画出相应图形(2)让学生通过实际操作与说理,理解直线和平面平行的判定定理;(3)通过例题和练习能利用线面平行解决有关平行的问题.学法指导:1. 直线与平面的位置关系有几种?2.要证直线与平面平行,需要证明什么问题?3.当直线平行于平面时,与内的一条直线的位置关系有哪些? 自学检测:1.直线 a//直线 b,b,则 a 与的位置关系是:( )A B C D2.是平面外的一条直线,可得出的条件是:( )A 内的一条直线不相交 B. 内的两条直线不相交C 内的无数条直线不相交 D 内的任意一条直线都不相交。3、过空间一点作与两条异面直线都平行的平面,这样的平面( )A 不存在 B 有且只有一个或不存在 C 有且只有一个 D 有无数个4、下列命题正确的为是_____________________(1)如果一条直线不在平面内,则这条直线与该面平行(2)过直线外一点,可以作无数个平面与该直线平行(3)过直线外一点,可以作无数条直线与该平面平行(4)如果一条直线与平面平行,则它与平面内的任意直线平行5.下面四个命题中:① 平面外的直线就是平面的平行线。②平行于同一平面的两条直线平行③ 若直线平行于直线,则直线平行于经过直线的任何平面。正确命题的序号是______________________6.已知长方体,求证:平面C1ABCDA1B1D1深化提高1、如图,已知为平行四边形所在平面外一点,为的中点,求证:平面.针对练习:在空间四面体中,分别为 各棱的中点, ①四边形是什么四边形?②若,四边形是什么四边形?③若,四边形是什么四边形?④ 直线与平面的位置关系是什么?请证明?例 2 如图,在四棱锥中,是平行四边形,,分别是,的中点.求证:平面.B针对练习:图示,是长方体底面对角线的交点,求证:.课堂小结:1.直线与平面的位置关系及符号表示(1)从直线与平面的公共点的个数可分为(2)这三种关系的图形表示及符号表示:图形: __________________ _____________________ __________________符号:_______________ _____________________ __________________2.直线与平面平行的判定定理:______________________________________________用符号语言可表示为______________________________________.其它判定直线与平面平行的方法:_____________________________________.【课堂小测试】1.已...