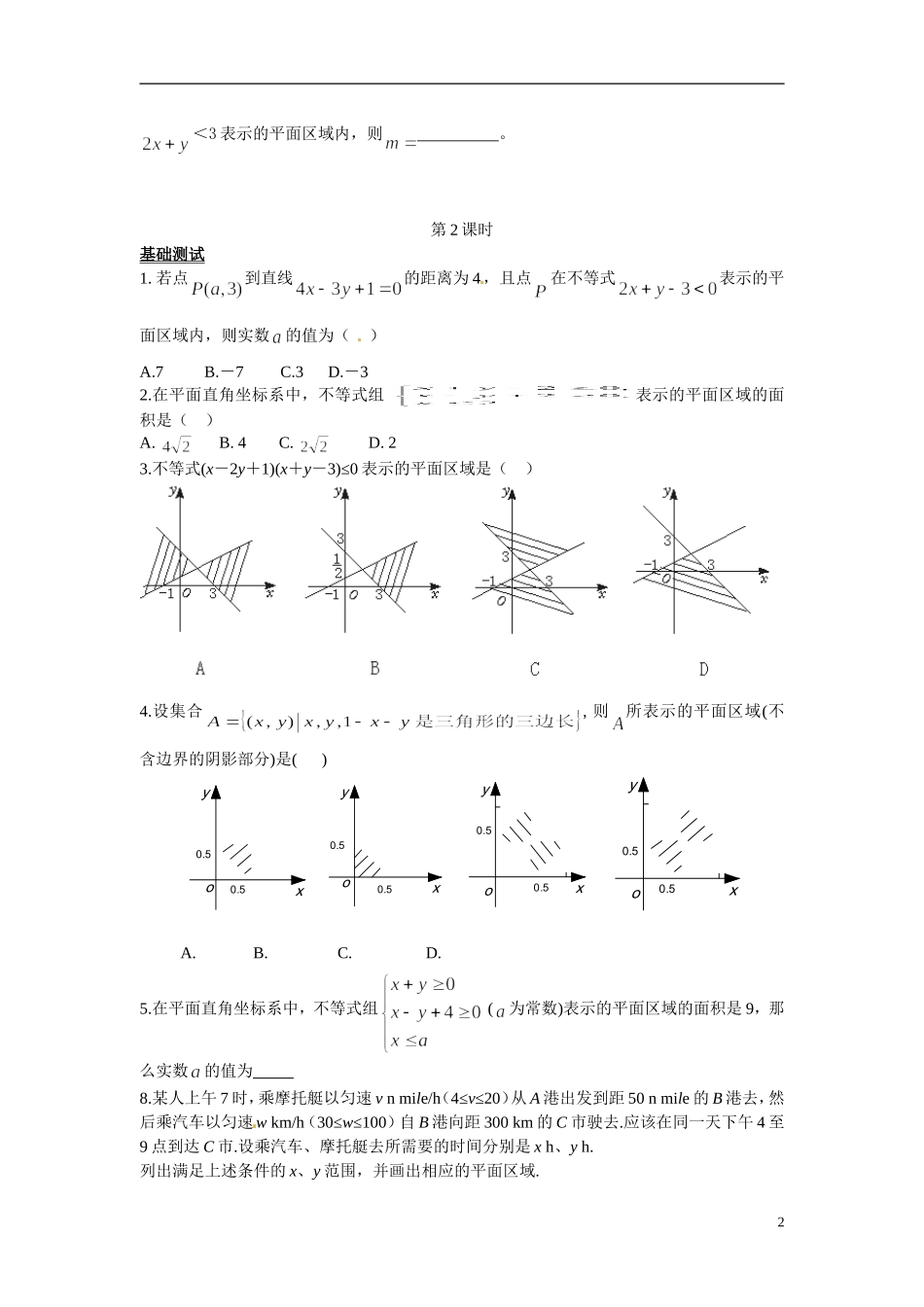
3.3.1 二元一次不等式(组)与平面区域第 1 课时基础测试1. 不在表示的平面区域内的点是( )A.(0,0) B.(1,2) B.(2,1) D.( 3,1)2.在平面直角坐标系中,点在直线的右上方,则的取值范围是( )A.(1,4)B.(-1,4)C.(-∞,4)D.(4,+∞)3. 下面四个点中,在平面区域内的点是( )A. B. C. D.4.在平面直角坐标系中,可表示满足不等式的点的集合(用阴影部分来表示)的是( ) 5. 若点(2,1)和(4,3)在直线0 的两侧,则 a 的取值范围是 .6.由直线,和围成的三角形区域(包括边界)用不等式(组)可表示为 。7. 画出不等式组表示的平面区域.8. 画出不等式组所表示的平面区域并求其面积.能力演练9.在平面直角坐标系中,若不等式组(为常数)所表示的平面区域的面积等于 2,则的值为( )A. -5 B. 1 C. 2 D. 3 w.w.10.(2010·北京文,11)若点到直线的距离为 4,且点在不等式1<3 表示的平面区域内,则 。第 2 课时基础测试1. 若点到直线的距离为 4,且点在不等式表示的平面区域内,则实数的值为( )A.7 B.-7 C.3 D.-32.在平面直角坐标系中,不等式组表示的平面区域的面积是( )A. B. 4 C. D. 23.不等式(x-2y+1)(x+y-3)≤0 表示的平面区域是( ) 4.设集合, 则所表示的平面区域(不含边界的阴影部分)是( ) A. B. C. D.5.在平面直角坐标系中,不等式组 (为常数)表示的平面区域的面积是 9,那么实数的值为 8.某人上午 7 时,乘摩托艇以匀速 v n mile/h(4≤v≤20)从 A 港出发到距 50 n mile 的 B 港去,然后乘汽车以匀速w km/h(30≤w≤100)自 B 港向距 300 km 的 C 市驶去.应该在同一天下午 4 至9 点到达 C 市.设乘汽车、摩托艇去所需要的时间分别是 x h、y h.列出满足上述条件的 x、y 范围,并画出相应的平面区域.oyx0.50.5oyx0.50.5oyx0.50.5oyx0.50.52能力演练9.已知{( , ) |6,0,0}x yxyxy ,{( , ) |4,0,20}Ax yxyxy,若向区域 上随机投一点 P ,则点 P 落入区域 A 的概率为( )A.31 B.32 C.91 D.9210.已知 D 是由不等式组,所确定的平面区域,则圆 在区域 D 内的弧长为( )A B C D11.若不等式组表示的平面区域是一个三角形,则的取值范围是 . 12.某矿山车队有 4 辆载重量为 10 t 的甲型卡车和 7 辆载重量为 6 t 的乙型卡车,有 9 ...