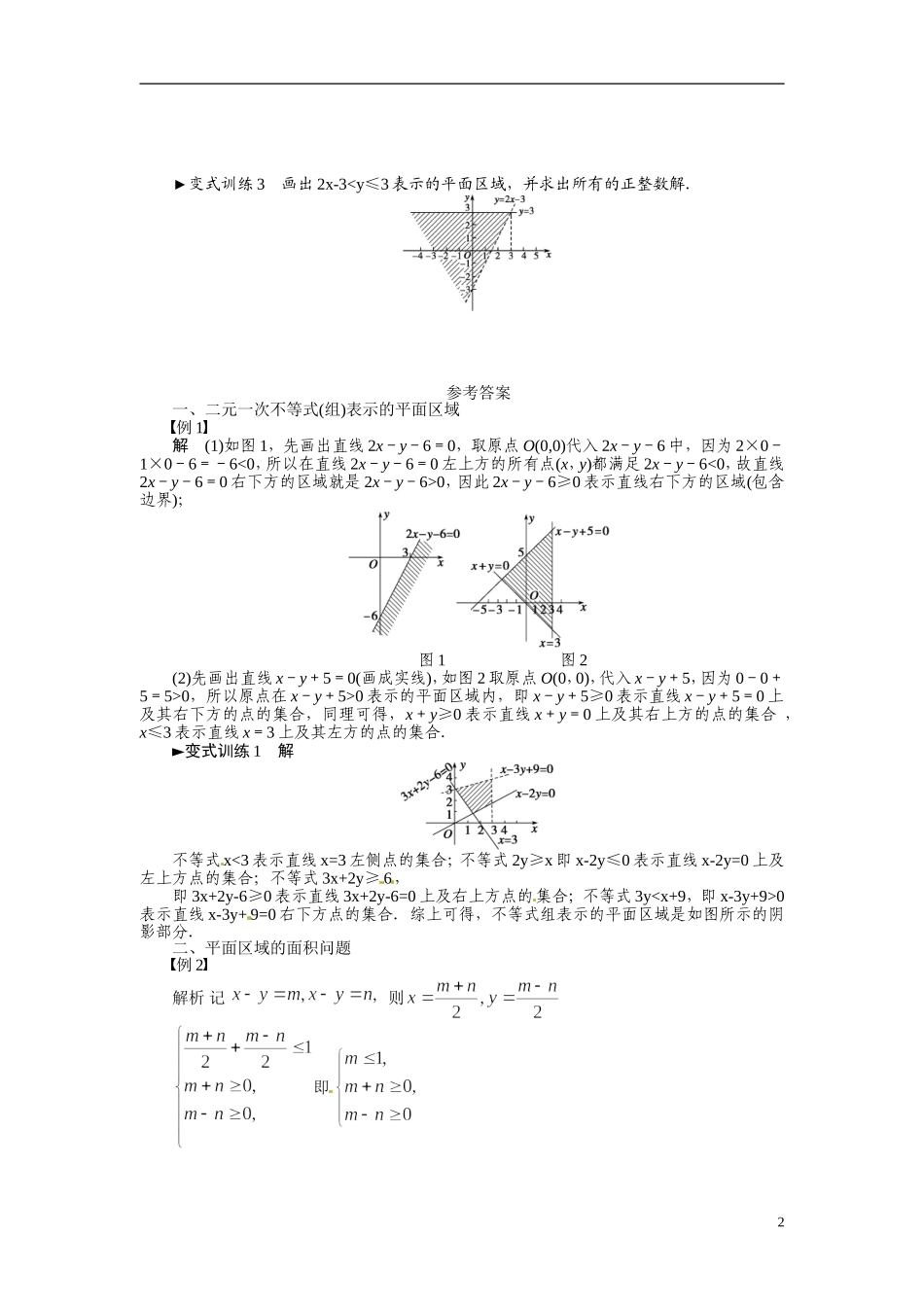
3.3 二元一次不等式(组)与简单的线性规划问题特色训练 一、二元一次不等式(组)表示的平面区域例 1 画出下列不等式(组)表示的平面区域.(1)2x-y-6≥0; (2)►变式训练 1 画出不等式组表示的区域.二、平面区域的面积问题例 2 在平面直角坐标系 xOy 中,已知平面区域 A={(x,y)|x+y≤1,且 x≥0,y≥0},则平面区域 B={(x+y,x-y)|(x,y)∈A}的面积为( ) A.2 B.1 C. D.►变式训练 2 若 A 为不等式组§表示的平面区域,则当 a 从-2 连续变化到 1 时,动直线x+y=a 扫过 A 中的那部分区域的面积为 .三、平面区域内的整点个数问题例 3 利用平面区域求不等式组的整数解.分析 先画出平面区域,再用代入法逐个验证.1►变式训练 3 画出 2x-30,因此 2x-y-6≥0 表示直线右下方的区域(包含边界); 图 1 图 2(2)先画出直线 x-y+5=0(画成实线),如图 2 取原点 O(0,0),代入 x-y+5,因为 0-0+5=5>0,所以原点在 x-y+5>0 表示的平面区域内,即 x-y+5≥0 表示直线 x-y+5=0 上及其右下方的点的集合,同理可得,x+y≥0 表示直线 x+y=0 上及其右上方的点的集合 ,x≤3 表示直线 x=3 上及其左方的点的集合.►变式训练 1 解 不等式x<3 表示直线 x=3 左侧点的集合;不等式 2y≥x 即 x-2y≤0 表示直线 x-2y=0 上及左上方点的集合;不等式 3x+2y≥ 6,即 3x+2y-6≥0 表示直线 3x+2y-6=0 上及右上方点的集合;不等式 3y0表示直线 x-3y+ 9=0 右下方点的集合.综上可得,不等式组表示的平面区域是如图所示的阴影部分.二、平面区域的面积问题例 2 解析 记 则即 2作出可行域可知面积为 1.答案 B►变式训练 2 答案 解析 如图所示,区域 A 表示的平面区域为△OBC 内部及其边界 组成的图形,当 a 从-2 连续变化到 1 时扫过的区域为四边形 ODEC 所围成的区域.又 D(0,1),B(0,2),E,C(2,0).S 四边形 ODEC=S△OBCS△BDE=.例 3 解 把 x=3 代入 6x+7y≤50,得y≤4,又 y...