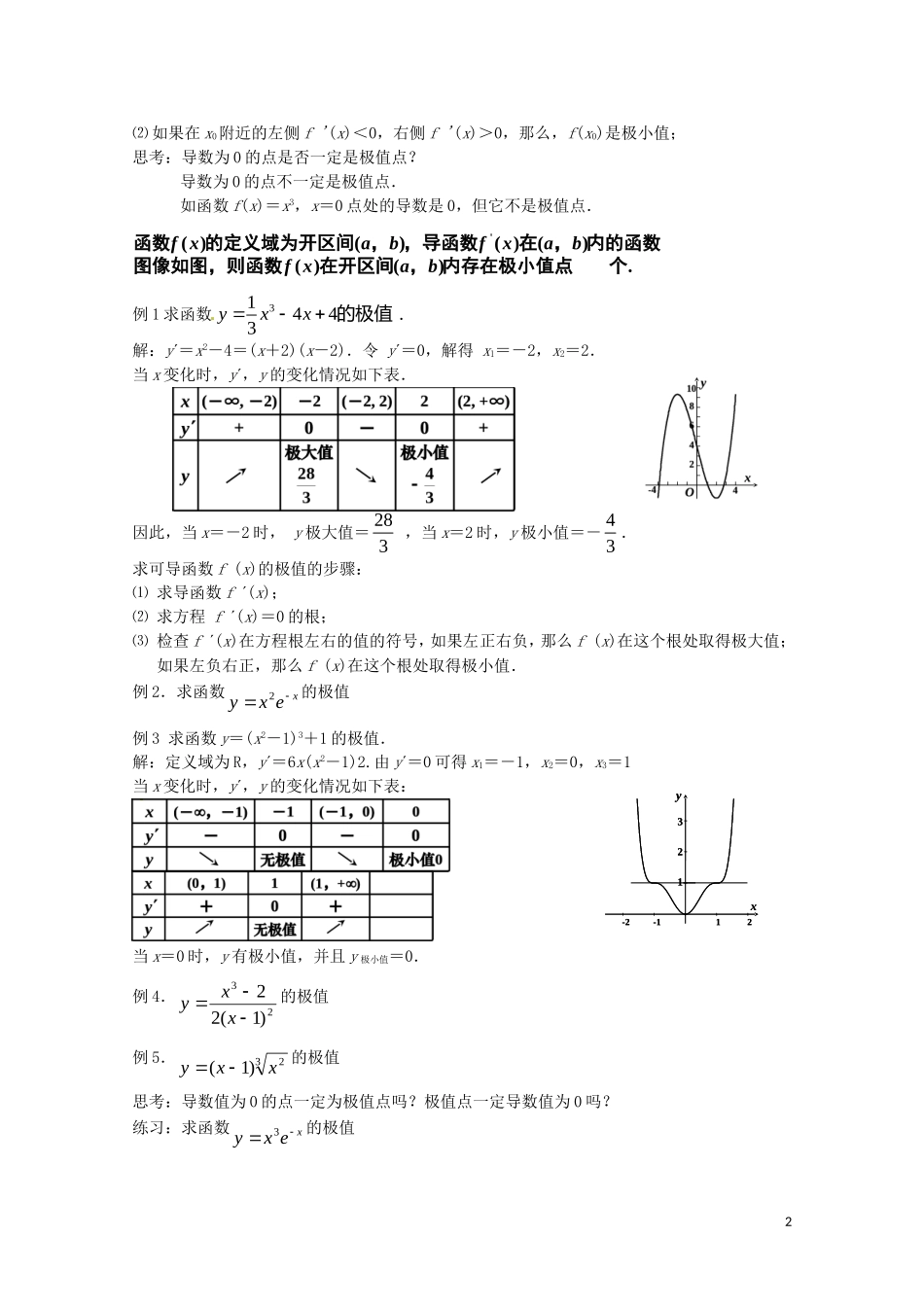
1.3.2 函数的极值与导数(1)一、教学目标:理解函数的极大值、极小值、极值点的意义.掌握函数极值的判别方法.进一步体验导数的作用.二、教学重点:求函数的极值.教学难点:严格套用求极值的步骤.三、教学过程:(一)函数的极值与导数的关系1、观察下图中的曲线a 点的函数值 f(a)比它临近点的函数值都大.b 点的函数值 f(b)比它临近点的函数值都小.2、观察函数 f(x)=2x3-6x2+7 的图象,思考:函数 y=f(x)在点 x=0,x=2 处的函数值,与它们附近所有各点处的函数值,比较有什么特点?(1)函数在 x=0 的函数值比它附近所有各点的函数值都大,我们说 f(0) 是函数的一个极大值;(2)函数在 x=2 的函数值比它附近所有各点的函数值都小,则 f(2)是函数的一个极小值.函数 y=2x3-6x2+7 的一个极大值: f (0); 一个极小值: f (2).函数 y=2x3-6x2+7 的 一个极大值点: ( 0, f (0) ); 一个极小值点: ( 2, f (2) ).3、极值的概念:一般地,设函数 f(x)在点 x0附近有定义,如果对 x0 附近的所有的点,都有 f(x)< f(x0)我们就说 f(x0)是函数 f(x)的一个极大值,记作 y 极大值=f(x0);如果对 x0附近的所有的点,都有 f(x)>f(x0)我们就说 f(x0)是函数 f(x)的一个极小值,记作 y 极小值=f(x0).极大值与极小值统称为极值.4、观察下图中的曲线考察上图中,曲线在极值点处附近切线的斜率情况.上图中,曲线在极值点处切线的斜率为 0,极大值点左侧导数为正,右侧为负;极小值点左侧导数为负,右侧为正.函数的极值点 xi是区间[a, b]内部的点,区间的端点不能成为极值点.函数的极大(小)值可能不止一个,并且函数的极大值不一定大于极小值,极小值不一定小于极大值.函数在[a, b]上有极值,其极值点的分布是有规律的,像相邻两个极大值间必有一个极小值点.5、利用导数判别函数的极大(小)值:一般地,当函数 f(x)在点 x0 处连续时,判别 f(x0)是极大(小)值的方法是:⑴ 如果在 x0附近的左侧 f '(x)>0,右侧 f '(x)<0,那么,f(x0)是极大值;1⑵ 如果在 x0附近的左侧 f '(x)<0,右侧 f '(x)>0,那么,f(x0)是极小值;思考:导数为 0 的点是否一定是极值点?导数为 0 的点不一定是极值点.如函数 f(x)=x3,x=0 点处的导数是 0,但它不是极值点..)()()()()()('个内存在极小值点,在开区间图像如图,则函数内的函数,在,导函数,的定义域为开区间...