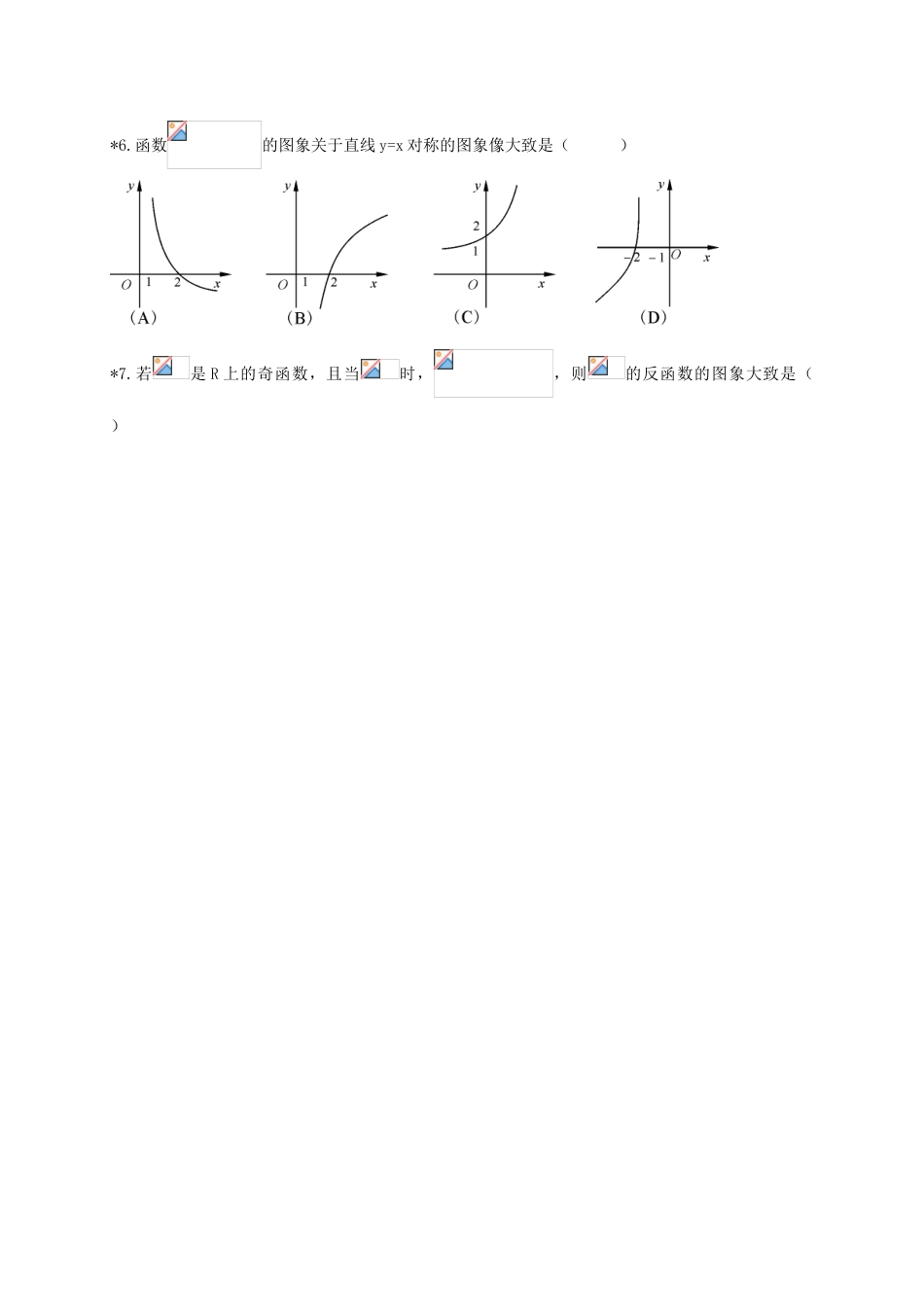
2014 高中数学 对数函数及其性质 3 导学案 新人教 A 版必修 1(六)对数函数及其性质(3)教学目标:1.了解反函数的概念,加深对函数思想的理解.2.进一步理解对数函数的定义,掌握对数函数的图象和性质。一、课前准备用列表描点法在同一个直角坐标点中画出的函数图象.…-2-1012……………-2-1012 二、新课导学(一)自主学习1.反函数的概念当一个函数是一一映射时,可以把这个函数的因变量作为一个新的函数 ,而把这个函数的自变量作为新的函数的 ,我们称这两个函数为反函数.函数的反函数是 ,函数的反函数是 ,函数>1)的反函数是 函数>0 且)的反函数是 函数>0关于直线 对称。(二)典型例题例题 1.求函数的值域(1) (2)xy(3)动手:求函数(1) (2)的值域例题 2.函数的单调性1、 求函数的单调区间和值域。2、 求函数的单调递减区间。三、反馈练习1.函数的值域为( )A. B. C. D. 2.函数的值域为 3.函数的定义域为 ; 的定义域为 4. 函数的定义域为 ;的定义域为 .5.已知函数的定义域为[-1,1],则函数的定义域为 *6.函数的图象关于直线 y=x 对称的图象像大致是( )*7.若是 R 上的奇函数,且当时,,则的反函数的图象大致是( )