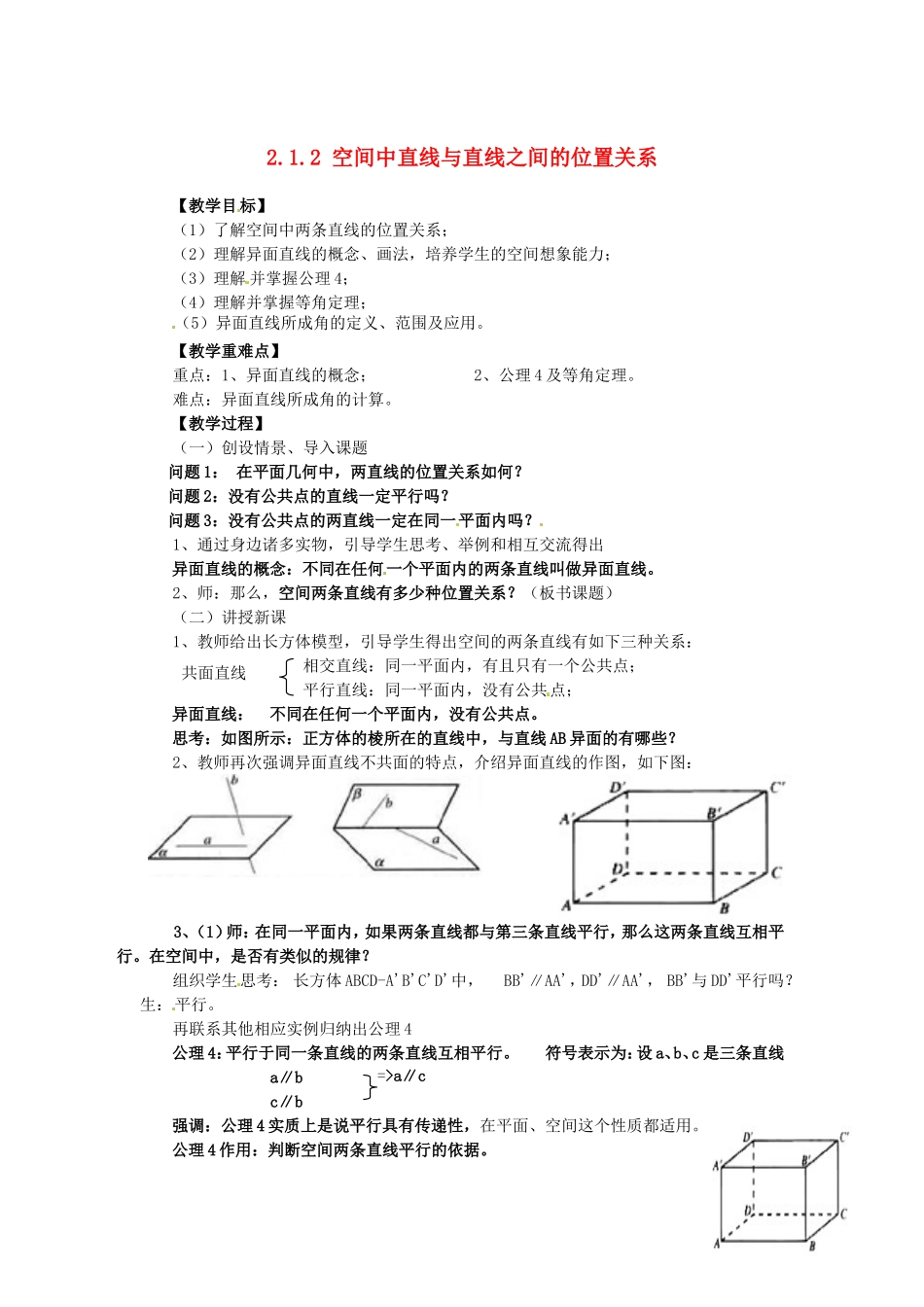
2.1.2 空间中直线与直线之间的位置关系【教学目标】(1)了解空间中两条直线的位置关系;(2)理解异面直线的概念、画法,培养学生的空间想象能力;(3)理解 并掌握公理 4; (4)理解并掌握等角定理;(5)异面直线所成角的定义、范围及应用。【教学重难点】重点:1、异面直线的概念; 2、公理 4 及等角定理。难点:异面直线所成角的计算。【教学过程】(一)创设情景、导入课题问题 1: 在平面几何中,两直线的位置关系如何?问题 2:没有公共点的直线一定平行吗?问题 3:没有公共点的两直线一定在同一平面内吗?1、通过身边诸多实物,引导学生思考、举例和相互交流得出异面直线的概念:不同在任何一个平面内的两条直线叫做异面直线。2、师:那么,空间两条直线有多少种位置关系?(板书课题)(二)讲授新课1、教师给出长方体模型,引导学生得出空间的两条直线有如下三种关系: 相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点。思考:如图所示:正方体的棱所在的直线中,与直线 AB 异面的有哪些?2、教师再次强调异面直线不共面的特点,介绍异面直线的作图,如下图: 3、(1)师:在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线互相平行。在空间中,是否有类似的规律?组织学生思考: 长方体 ABCD-A'B'C'D'中, BB'∥AA',DD'∥AA', BB'与 DD'平行吗?生:平行。 再联系其他相应实例归纳出公理 4公理 4:平行于同一条直线的两条直线互相平行。 符号表示为:设 a、b、c 是三条直线a∥bc∥b强调:公理 4 实质上是说平行具有传递性,在平面、空间这个性质都适用。公理 4 作用:判断空间两条直线平行的依据。1共面直线 =>a∥c例 1 空间四边形 ABCD 中,E.F.G.H 分别是 AB.BC.CD.DA 的中点求证:四边形 EFGH 是平行四边形证明:连接 BD因为 EH 是△ABD 的中位线,所以 EH∥BD 且 EH= 21 BD 同理 FG∥BD 且 FG= 21 BD因为 EH∥FG 且 EH=FG所以四边形 EFGH 是平行四边形点评:例 2 的讲解让学生掌握了公理 4 的运用变式:在例 1 中如果加上条件 AC=BD,那么四边形 EFGH 是什么图形?4、组织学生思考教材 P46 的思考题 让学生观察、思考:∠ADC 与 A'D'C'、∠ADC 与∠A'B'C'的两边分别对应平行,这两组角的大小关系如何?生:∠ADC = A'D'C',∠ADC + ∠A'B'C' = 1...