2014高中数学（教案+课内预习学案+课内探究学案+课后练习与提高）2.3.2抛物线的简单几何性质 新人教A版选修1-1

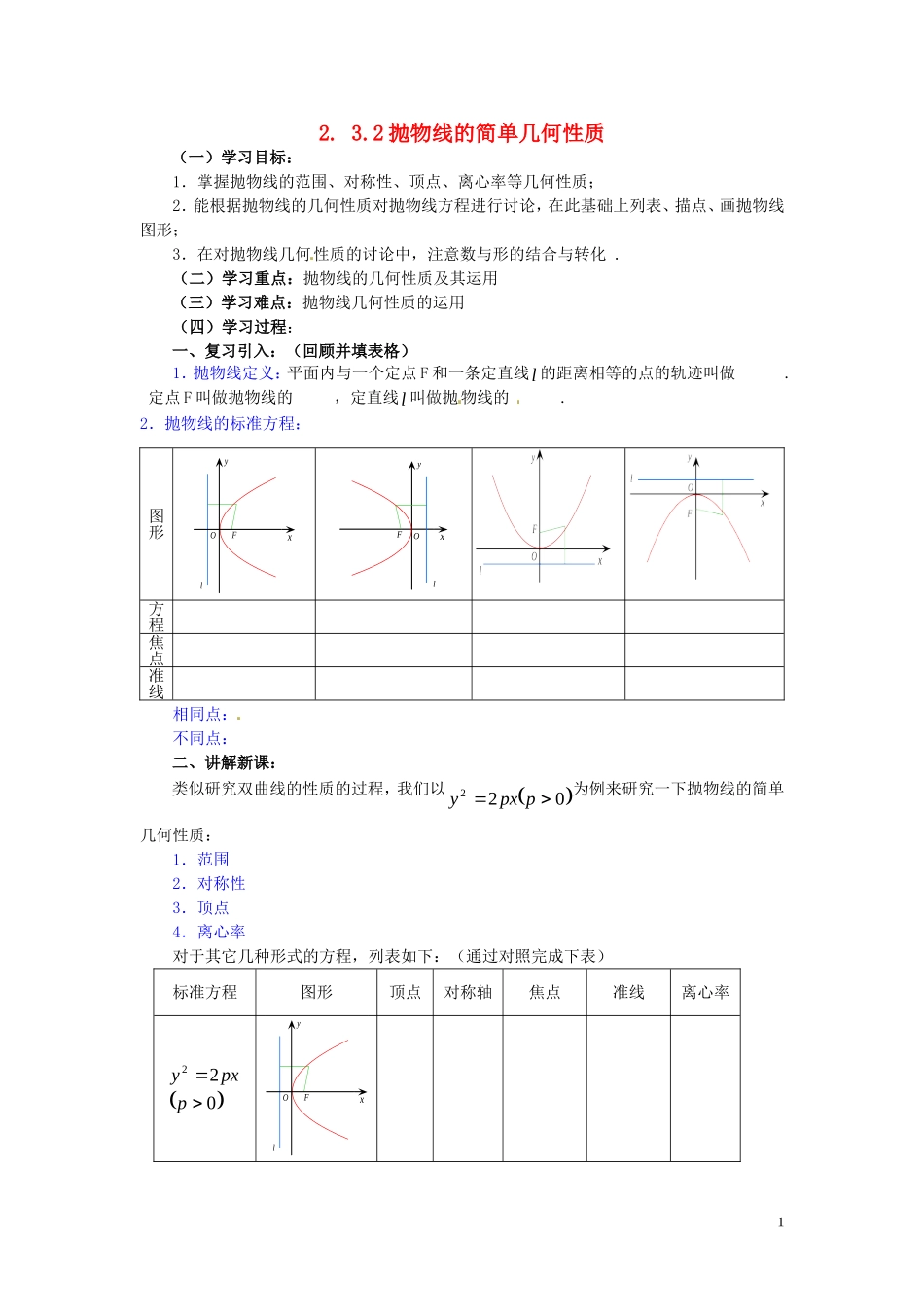
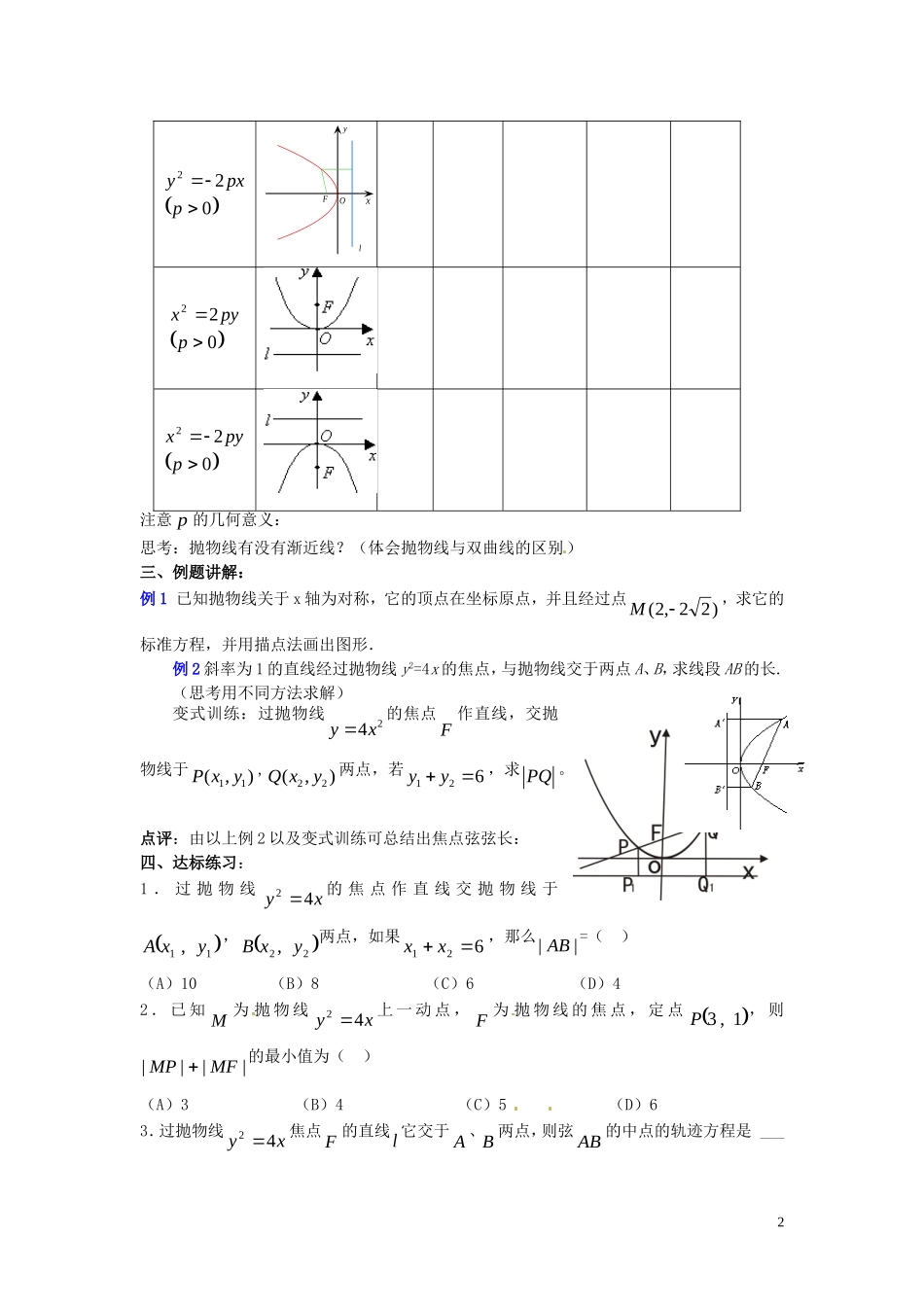
2. 3.2 抛物线的简单几何性质（一）学习目标：1．掌握抛物线的范围、对称性、顶点、离心率等几何性质；2．能根据抛物线的几何性质对抛物线方程进行讨论，在此基础上列表、描点、画抛物线图形；3．在对抛物线几何性质的讨论中，注意数与形的结合与转化 .（二）学习重点：抛物线的几何性质及其运用（三）学习难点：抛物线几何性质的运用 （四）学习过程：一、复习引入：（回顾并填表格） 1．抛物线定义：平面内与一个定点 F 和一条定直线l 的距离相等的点的轨迹叫做 . 定点 F 叫做抛物线的 ，定直线l 叫做抛物线的 .2．抛物线的标准方程： 相同点：不同点：二、讲解新课：类似研究双曲线的性质的过程，我们以022ppxy为例来研究一下抛物线的简单几何性质：1．范围2．对称性3．顶点4．离心率对于其它几种形式的方程，列表如下：（通过对照完成下表）标准方程图形顶点对称轴焦点准线离心率022ppxyxyOFl图形xyOFlxyOFl方程焦点准线1022ppxyxyOFl022ppyx022ppyx注意 p 的几何意义：思考：抛物线有没有渐近线？（体会抛物线与双曲线的区别）三、例题讲解：例 1 已知抛物线关于 x 轴为对称，它的顶点在坐标原点，并且经过点)22,2( M，求它的标准方程，并用描点法画出图形．例 2 斜率为 1 的直线经过抛物线 y2=4x 的焦点，与抛物线交于两点 A、B，求线段 AB 的长.（思考用不同方法求解）变式训练：过抛物线24yx的焦点F作直线，交抛物线于11( ,)P x y,22(,)Q xy两点，若126yy ，求 PQ 。点评：由以上例 2 以及变式训练可总结出焦点弦弦长：四、达标练习：1 ． 过 抛 物 线xy42 的 焦 点 作 直 线 交 抛 物 线 于11 , yxA， 22, yxB两点，如果621 xx，那么|| AB =（ ）（A）10 （B）8 （C）6 （D）42 ． 已 知 M 为 抛 物 线xy42 上 一 动 点 ， F 为 抛 物 线 的 焦 点 ， 定 点1,3P， 则||||MFMP 的最小值为（ ）（A）3 （B）4 （C）5 （D）63．过抛物线xy42 焦点 F 的直线l 它交于 A 、B 两点，则弦 AB 的中点的轨迹方程是 ___2___ 4.定长为3 的线段 AB 的端点 A 、B 在抛物线xy2上移动，求 AB 中点 M 到 y 轴距离的最小值，并求出此时 AB 中点 M 的坐标.参考答案：1. B 2. B 3.122xy 4. 22,45M , M 到...