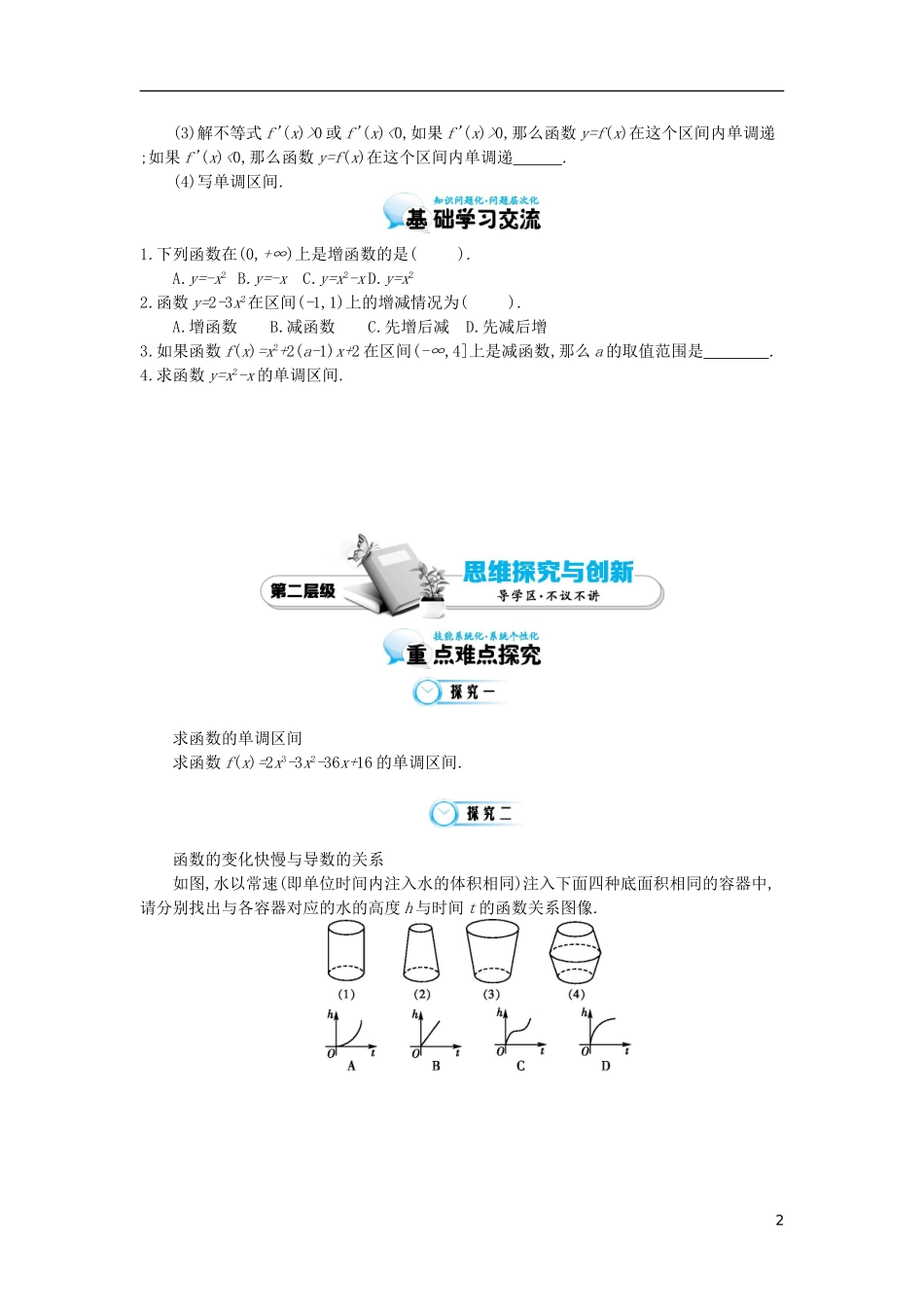
第 1 课时 导数与函数的单调性1.结合实例,直观探索并掌握函数的单调性与导数的关系.2.会利用导数判断函数的单调性.3.会利用导数求函数的单调区间.对于函数 y=x3-3x,如何判断单调性呢?你能画出该函数的图像吗?定义法是解决问题的最根本方法,但定义法较繁琐,又不能画出它的图像,那该如何解决呢?问题 1: 增函数和减函数一般地,设函数 f(x)的定义域为 I:如果对于定义域 I 内某个区间 D 上的任意两个自变量的值 x1、x2,当 x1f(x2),那么就说函数 f(x)在区间 D 上是 .(如图(2)所示) 问题 2:单调性与单调区间如果一个函数在某个区间 M 上是单调增函数或是单调减函数,就说这个函数在这个区间M 上具有 ,区间 M 称为 . 问题 3:判断函数的单调性有 和 ,图像法是作出函数图像,利用图像找出上升或下降的区间,得出结论.奇函数在两个对称的区间上具有 的单调性;偶函数在两个对称的区间上具有 的单调性.定义法是利用函数单调性的定义进行判断,通过设变量、作差、变形、定号,得出结论. 作图并观察函数的图像,找出图像上升(或下降)的起点和终点的 坐标,从而得出单调递增(或递减)区间. 问题 4:根据导数与函数单调性的关系,在函数定义域的某个区间(a,b)内求函数单调区间的一般步骤:(1)确定函数 f(x)的定义域.(2)求导数 f'(x).1(3)解不等式 f'(x)>0 或 f'(x)<0,如果 f'(x)>0,那么函数 y=f(x)在这个区间内单调递 ;如果 f'(x)<0,那么函数 y=f(x)在这个区间内单调递 . (4)写单调区间.1.下列函数在(0,+∞)上是增函数的是( ).A.y=-x2 B.y=-xC.y=x2-x D.y=x22.函数 y=2-3x2在区间(-1,1)上的增减情况为( ).A.增函数B.减函数C.先增后减D.先减后增3.如果函数 f(x)=x2+2(a-1)x+2 在区间(-∞,4]上是减函数,那么 a 的取值范围是 . 4.求函数 y=x2-x 的单调区间.求函数的单调区间求函数 f(x)=2x3-3x2-36x+16 的单调区间.函数的变化快慢与导数的关系如图,水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中,请分别找出与各容器对应的水的高度 h 与时间 t 的函数关系图像.2含有参数的函数单调性问题已知函数 f(x)=x3+ax2+x+1,a∈R.(1)讨论函数 f(x)的单调区间;(2)设函数 f(x)在区间(- ,- )内是减函数,求 a 的取值范...