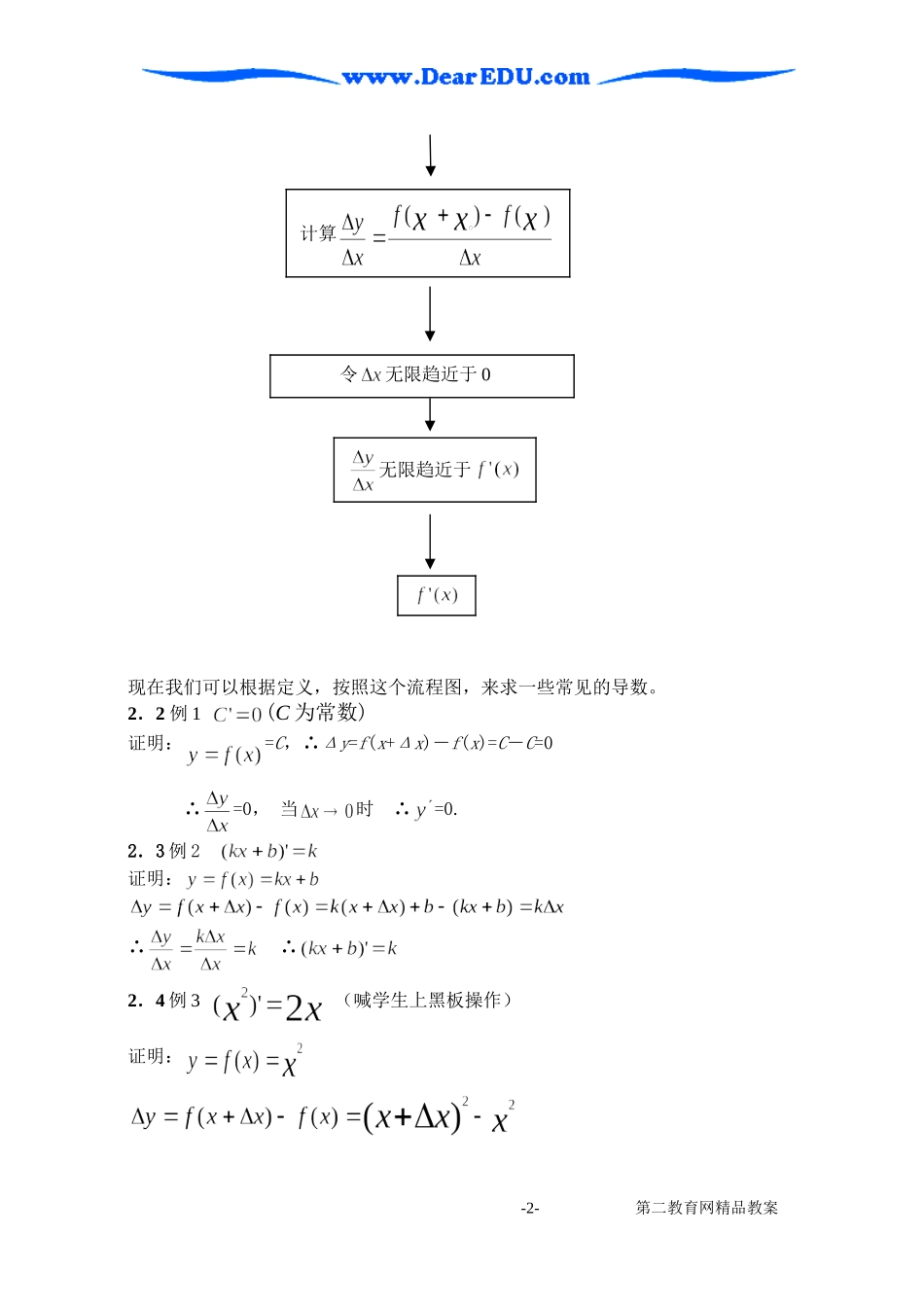
§3.2 几种常见函数的导数教学目的:1.理解公式的证明过程。2.学会利用公式,求一些函数的导数。教学重点:用定义推导常见函数的导数公式教学难点:基本初等函数的应用授课类型:新授课 课时安排:1 课时 教 具:实物投影仪 教学过程:1、复习引入: 1.1 导数的概念:设函数在区间(a,b)上有定义, ∈(a,b),当时,比值无限趋近于一个常数 A,则称 f(x)在点处可导,并称该常数 A 为函数 f(x)在点处的导数,记作 。1.2 导数的几何意义:是曲线上点()处的切线的斜率奎屯王新敞新疆因此,如果在 点可 导 , 则 曲 线在 点 () 处 的 切 线 方 程 为奎屯王新敞新疆1.3 导函数(导数):如果函数在区间内的任何一点处都可导,则f(x)在各点的导数也随着自变量 x 的变化而变化,因而也是自变量 x 的函数,称这个函数为函数的导函数,简称导数,也可记作,即。导数与导函数都称为导数,这要加以区分:求一个函数的导数,就是求导函数;求一个函数在给定点的导数,就是求导函数值奎屯王新敞新疆它们之间的关系是函数在点处的导数就是导函数在点的函数值奎屯王新敞新疆2、新课:2.1 求函数导数的流程图同学们,我们根据导数的概念,可以得到一个求函数导数的流程图。-1- 第二教育网精品教案给定函数 y = f (x)现在我们可以根据定义,按照这个流程图,来求一些常见的导数。2.2 例 1 (C 为常数)证明:=C,∴Δy=f(x+Δx)-f(x)=C-C=0∴=0, 当时 ∴=0.2.3 例 2 证明:∴ ∴2.4 例 3 (喊学生上黑板操作)证明:-2- 第二教育网精品教案计算无限趋近于令无限趋近于 0当时,,∴2.5 例 4 (喊学生上黑板操作)证明:当时,,∴2.6 练习:(喊学生上黑板做,作适当的提示)求证:(1) (2) 通过上面的这些题目,同学们可以发现一个什么规律?即此外,还有一些初等函数的导数,大家可以记忆一下。且3、练习-3- 第二教育网精品教案3.1 课时训练/课堂练习 1、2、3(喊三个同学上黑板操练)1、A2、C3、C3.2 课时训练/课堂例题 3(喊学生说,我在黑板写)注:三角公式的复习在这个地方需要适量的加强! 4、小结4.1 公式的推导(利用定义)4.2 初等函数的导数的记忆5、作业:课时训练上剩余的题目做完。 -4- 第二教育网精品教案