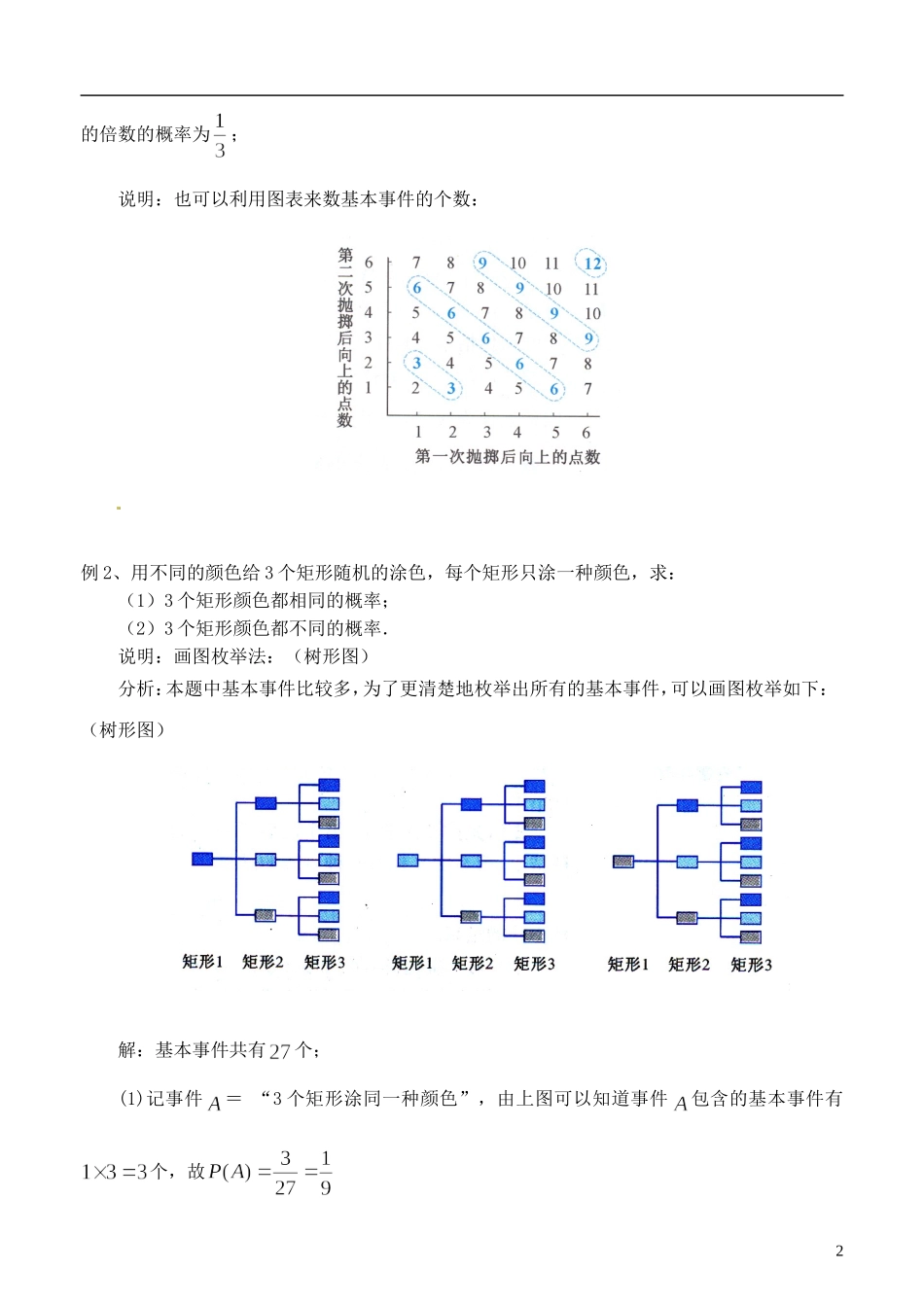
古典概型教学目标:(1)进一步掌握古典概型的计算公式;(2)能运用古典概型的知识解决一些实际问题;教学重点、难点:古典概型中计算比较复杂的背景问题.教学过程:一、问题情境问题:从甲、乙、丙三人中任选两名代表,求甲被选的概率?二、数学运用(枚举法算等可能事件的个数)例 1、将一颗骰子先后抛掷两次,观察向上的点数,问:(1)共有多少种不同的结果?(2)两数的和是 3 的倍数的结果有多少种?(3)两数和是 3 的倍数的概率是多少?说明:也可以利用图表来数基本事件的个数.解:(1)将骰子抛掷1次,它出现的点数有这 6 中结果。先后抛掷两次骰子,第一次骰子向上的点数有 6 种结果,第 2 次又都有 6 种可能的结果,于是一共有种不同的结果;(2)第 1 次抛掷,向上的点数为这 6 个数中的某一个,第 2 次抛掷时都可以有两种结果,使向上的点数和为 3 的倍数(例如:第一次向上的点数为 4,则当第 2 次向上的点数为 2或 5 时,两次的点数的和都为 3 的倍数),于是共有种不同的结果.(3)记“向上点数和为 3 的倍数”为事件,则事件的结果有种,因为抛两次得到的36 中结果是等可能出现的,所以所求的概率为答:先后抛掷 2 次,共有 36 种不同的结果;点数的和是 3 的倍数的结果有种;点数和是1的倍数的概率为;说明:也可以利用图表来数基本事件的个数:例 2、用不同的颜色给 3 个矩形随机的涂色,每个矩形只涂一种颜色,求:(1)3 个矩形颜色都相同的概率;(2)3 个矩形颜色都不同的概率.说明:画图枚举法:(树形图)分析:本题中基本事件比较多,为了更清楚地枚举出所有的基本事件,可以画图枚举如下:(树形图)解:基本事件共有个;(1)记事件= “3 个矩形涂同一种颜色”,由上图可以知道事件包含的基本事件有个,故2(2)记事件=“3 个矩形颜色都不同”,由上图可以知道事件包含的基本事件有个,故答:3个矩形颜色都相同的概率为;3 个矩形颜色都不同的概率为.说明:古典概型解题步骤:(1)阅读题目,搜集信息;(2)判断是否是等可能事件,并用字母表示事件;(3)求出基本事件总数和事件所包含的结果数;(4)用公式求出概率并下结论.例 3、一个各面都涂有色彩的正方体,被锯成个同样大小的小正方体,将这些正方体混合后,从中任取一个小正方体,求:(1)有一面涂有色彩的概率;(2)有两面涂有色彩的概率;(3)有三面涂有色彩的概率。解:在个小正方体中,一面图有色彩...