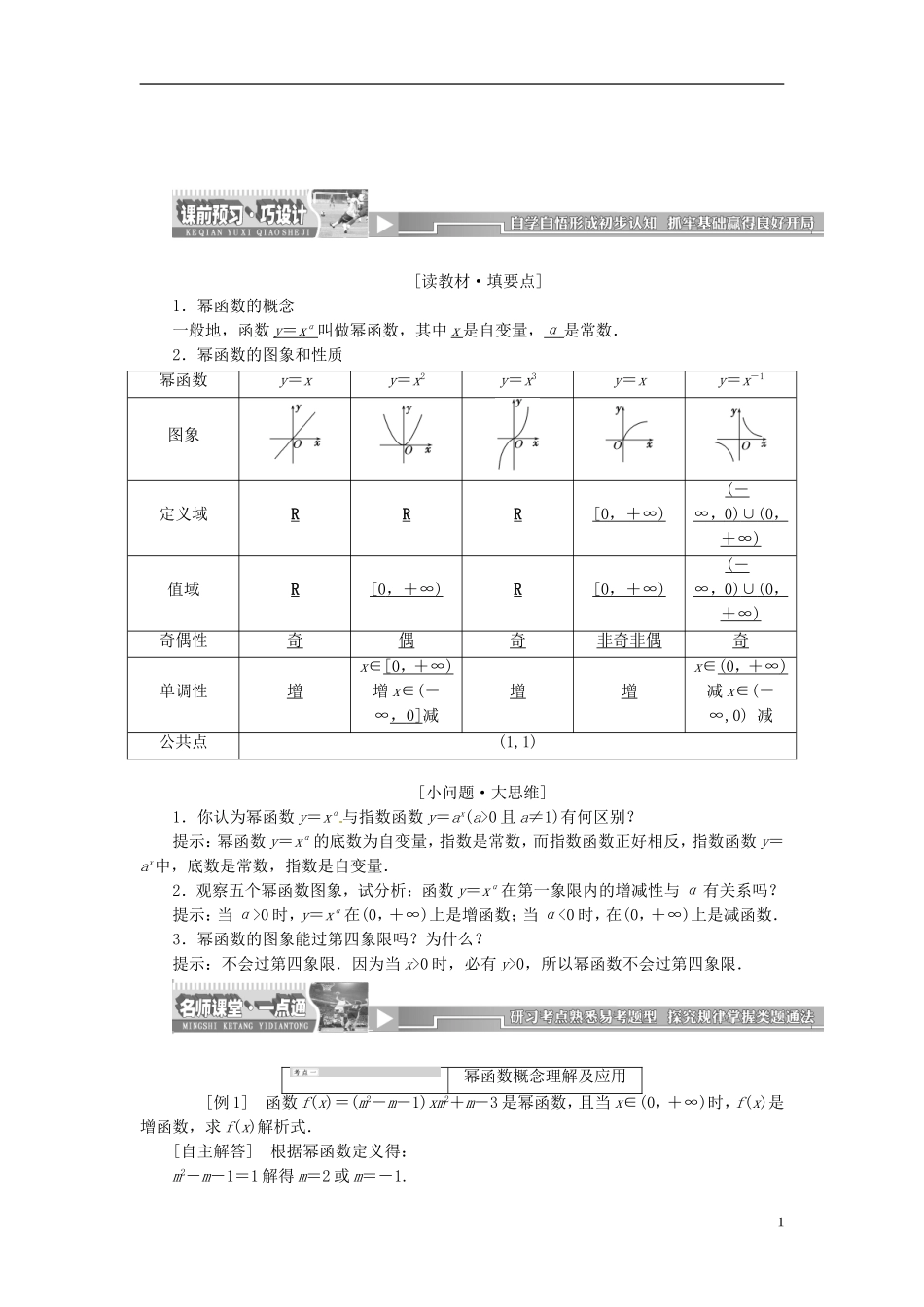
[读教材·填要点]1.幂函数的概念一般地,函数 y = x α 叫做幂函数,其中 x 是自变量,α 是常数.2.幂函数的图象和性质幂函数y=xy=x2y=x3y=xy=x-1图象定义域RRR[0 ,+∞ ) ( - ∞, 0) ∪ (0 , +∞ ) 值域R[0 ,+∞ ) R[0 ,+∞ ) ( - ∞, 0) ∪ (0 , +∞ ) 奇偶性奇偶奇非奇非偶奇单调性增x∈[0 ,+∞ ) 增 x∈(-∞, 0] 减增增x∈(0 ,+∞ ) 减 x∈(-∞,0) 减公共点(1,1) [小问题·大思维]1.你认为幂函数 y=xα与指数函数 y=ax(a>0 且 a≠1)有何区别?提示:幂函数 y=xα的底数为自变量,指数是常数,而指数函数正好相反,指数函数 y=ax中,底数是常数,指数是自变量.2.观察五个幂函数图象,试分析:函数 y=xα在第一象限内的增减性与 α 有关系吗?提示:当 α>0 时,y=xα在(0,+∞)上是增函数;当 α<0 时,在(0,+∞)上是减函数.3.幂函数的图象能过第四象限吗?为什么?提示:不会过第四象限.因为当 x>0 时,必有 y>0,所以幂函数不会过第四象限.幂函数概念理解及应用 [例 1] 函数 f(x)=(m2-m-1)xm2+m-3 是幂函数,且当 x∈(0,+∞)时,f(x)是增函数,求 f(x)解析式.[自主解答] 根据幂函数定义得:m2-m-1=1 解得 m=2 或 m=-1.1当 m=2 时,f(x)=x3在(0,+∞)上为增函数;当 m=-1 时,f(x)=x-3在(0,+∞)是减函数不符合要求.故 f(x)=x3.将例 1 中“f(x)是增函数”改为“f(x)是减函数”,求 f(x)解析式.解:由上述解答中可知当 m=-1 时 f(x)=x-3在(0,+∞)是减函数.∴f(x)=x-3. ——————————————————幂函数 y=xαα∈R,其中 α 为常数,其本质特征是以幂的底 x 为自变量,指数 α 为常数也可以为0. 这是判断一个函数是否为幂函数的重要依据和唯一标准.对例 1 来说,还要根据单调性验根,以免增根.————————————————————————————————————————1.已知函数 f(x)=(m2+2m)·xm2+m-1,m 为何值时,f(x)是:(1)正比例函数;(2)反比例函数;(3)二次函数;(4)幂函数.解:(1)若 f(x)为正比例函数,则⇒m=1.(2)若 f(x)为反比例函数,则⇒m=-1.(3)若 f(x)为二次函数,则⇒m=.(4)若 f(x)为幂函数,则 m2+2m=1,∴m=-1±.幂函数图象及应用[例 2] 如图所示的曲线是幂函数 y=xα在第一...