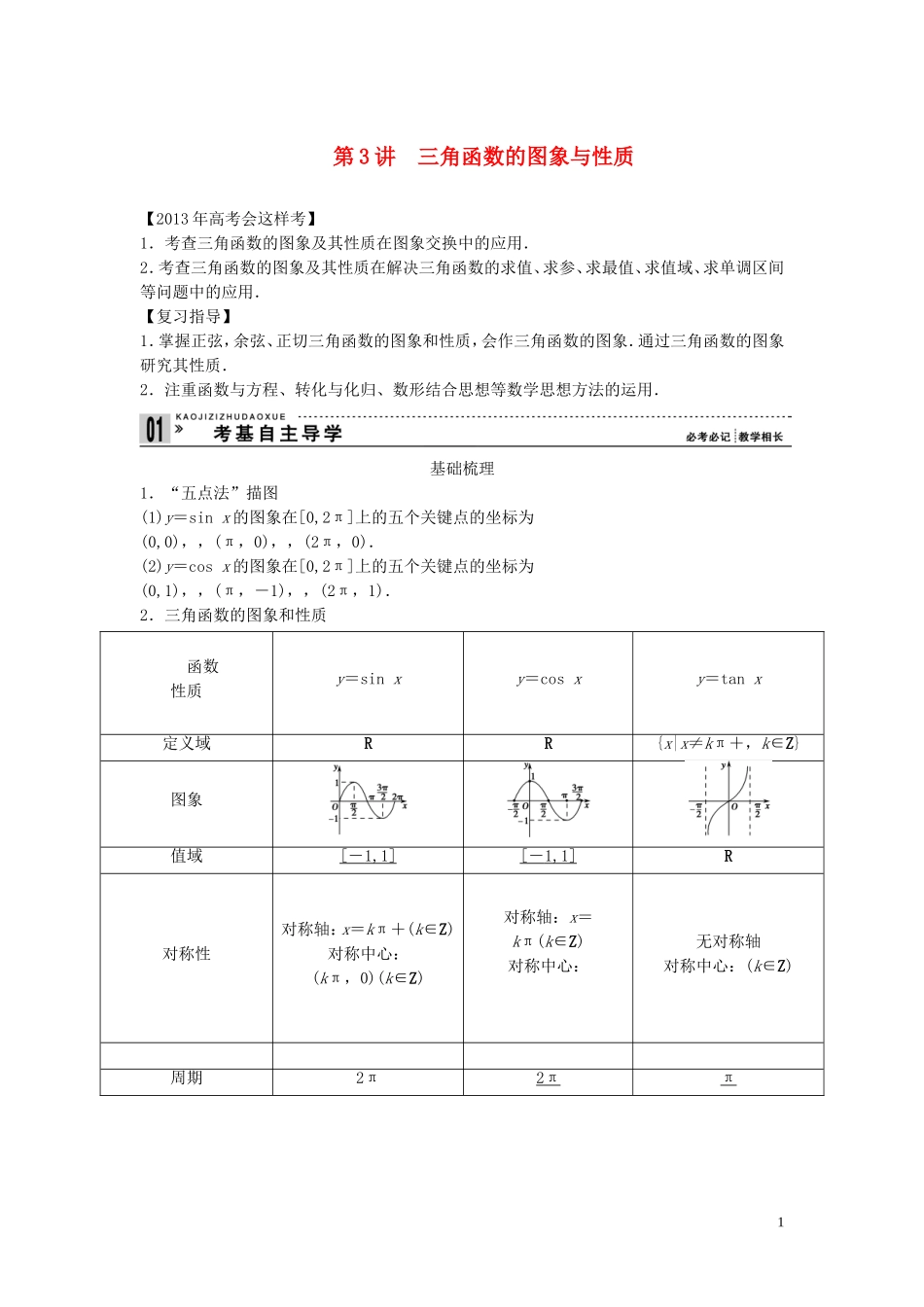
第 3 讲 三角函数的图象与性质【2013 年高考会这样考】1.考查三角函数的图象及其性质在图象交换中的应用.2.考查三角函数的图象及其性质在解决三角函数的求值、求参、求最值、求值域、求单调区间等问题中的应用.【复习指导】1.掌握正弦,余弦、正切三角函数的图象和性质,会作三角函数的图象.通过三角函数的图象研究其性质.2.注重函数与方程、转化与化归、数形结合思想等数学思想方法的运用.基础梳理1.“五点法”描图(1)y=sin x 的图象在[0,2π]上的五个关键点的坐标为(0,0),,(π,0),,(2π,0).(2)y=cos x 的图象在[0,2π]上的五个关键点的坐标为(0,1),,(π,-1),,(2π,1).2.三角函数的图象和性质 函数性质 y=sin xy=cos xy=tan x定义域RR{x|x≠kπ+,k∈Z}图象值域[ - 1,1] [ - 1,1] R对称性对称轴:x=kπ+(k∈Z)对称中心:(kπ,0)(k∈Z)对称轴:x=kπ(k∈Z)对称中心:无对称轴对称中心:(k∈Z)周期2π2ππ1单调性单调增区间,2kπ+(k∈Z);单调减区间,2kπ+(k∈Z)单调增区间[2kπ-π,2kπ](k∈Z);单调减区间[2kπ,2kπ+π](k∈Z)单调增区间,kπ+(k∈Z)奇偶性奇偶奇两条性质(1) 周期性 函数 y = A sin( ωx + φ ) 和 y = A cos( ωx + φ ) 的最小正周期为, y = tan( ωx + φ ) 的最小正周 期为 . (2) 奇偶性 三角函数中奇函数一般可化为 y = A sin ωx 或 y = A tan ωx ,而偶函数一般可化为 y = A cos ωx + b 的形式. 三种方法求三角函数值域 ( 最值 ) 的方法: (1) 利用 sin x 、 cos x 的有界性; (2) 形式复杂的函数应化为 y = A sin( ωx + φ ) + k 的形式逐步分析 ωx + φ 的范围,根据正 弦函数单调性写出函数的值域;(3) 换元法:把 sin x 或 cos x 看作一个整体,可化为求函数在区间上的值域 ( 最值 ) 问题. 双基自测1.(人教 A 版教材习题改编)函数 y=cos,x∈R( ).A.是奇函数B.是偶函数C.既不是奇函数也不是偶函数D.既是奇函数又是偶函数答案 C2.函数 y=tan 的定义域为( ).A. B.C. D.答案 A3.(2011·全国新课标)设函数 f(x)=sin(ωx+φ)+cos(ωx+φ)的最小正周期为 π,且f(-x)=f(x),则( ).A.f(x)在单调递减B.f(x)在单调递减2C.f(x)在单调递增D.f(x)在单调递增解析 f(x)=sin(ωx+φ)+cos(ωx+...