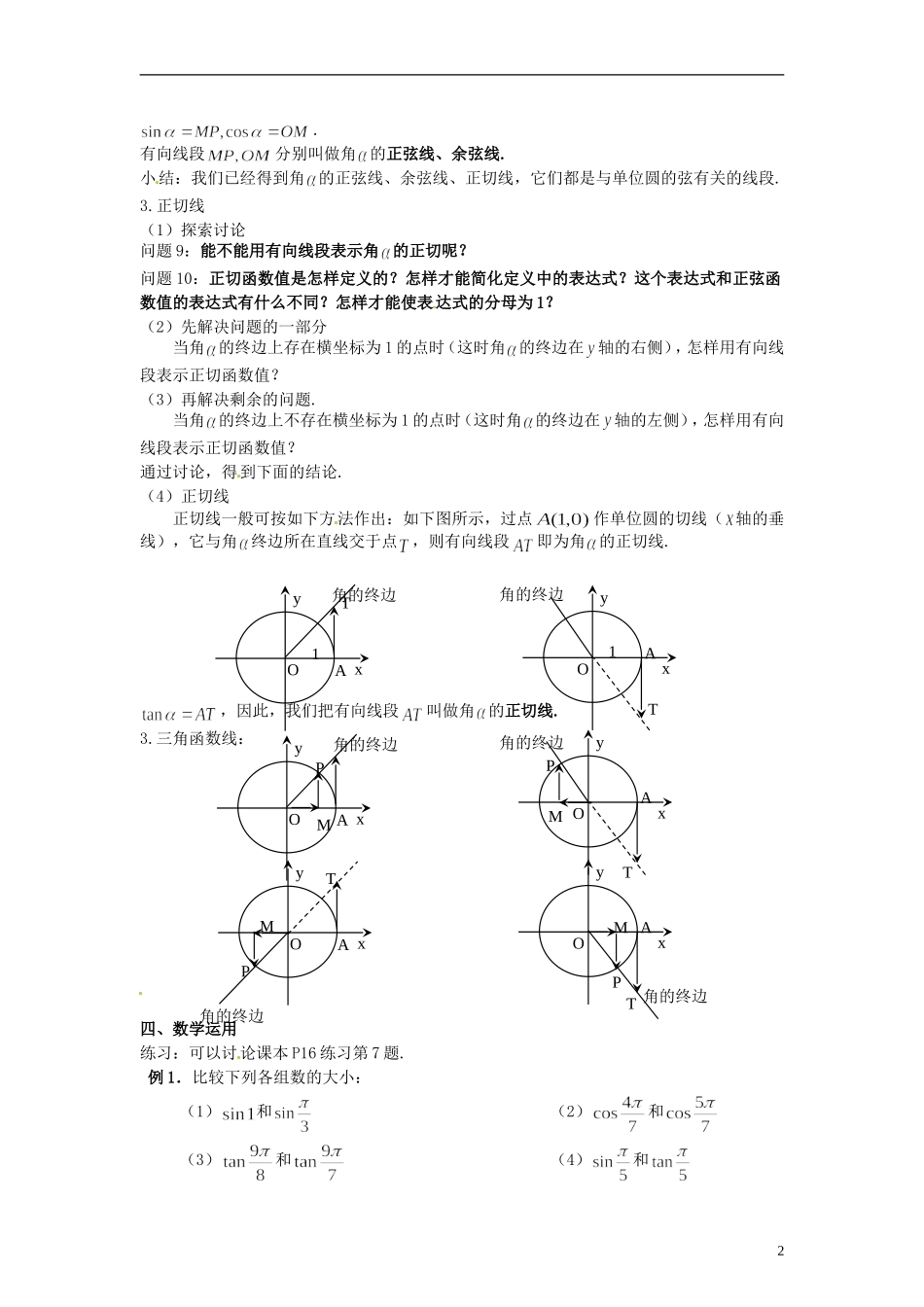
§1.2.1 任意角的三角函数(2)教学目标:理解并掌握有向线段的概念;正确利用与单位圆有关的有向线段,将任意角的正弦、余弦、正切函数值表示出来,即用正弦线、余弦线、正切线表示出来.教学重点:正弦、余弦、正切函数值的几何表示.教学难点:正弦、余弦、正切函数值的几何表示.教学过程:一、问题情境1.情境引入:我们已学过任意角三角函数,给出了任意角的正弦、余弦、正切的定义.2.提出问题:能不能用几何元素表示三角函数值?例如,能不能用线段表示三角函数值?二、学生 活动学生思考,讨论,回答.讨论可能沿着下面的方向进行:1.通过联想,可以提出问题 1:在初中,我们知道锐角三角函数可以看成线段的比,那么,任意角的三角函数是否可以也看成是线段的比呢?2.明确问题,可以提出问题 2:问题 1 的实际意义是什么?什么叫做三角函数?任意角的三角函数是怎样定义的?由此可以进一步明确问题 1 的意义.具体地,以正弦函数为例,当前的问题就是怎样用几何元素表示.(这里的是角终边上任一点的坐标)2.简化问题,可以提出问题 3:能进一步简化问题吗?是否可以在角的终边上取一个特殊点,使得三角函数值的表达式更为简单?结论是,当点在以原点为圆心,半径为 1 的圆(单位圆)上时,,而的函数值分别为点的纵坐标和横坐标 .三、建构数学1.有向线段(1)提出解决问题 1 的关键就这样解决问题 4:怎样表示点的纵,横坐标?能不能用线段表示坐标?围绕着如下问题进行讨论:问题 5:坐标是什么?问题 6:能不能用线段表示坐标?能不能用线段表示数?怎样才能做到这点?问题 7:和初中的锐角三角函数相比,我们现在面临的情况有什么不同?通过讨论,得到以下共识:为了用线段表示数,我们需要规定线段的方向.(2)给出有向线段、有向线段的数量、有向线段的长度的概念.下图 轴上,的数量分别是多少?有向线段的数量:.2.正弦线和余弦线(1)问题 8:怎样用有向线段表示正弦函数值?围绕着问题 8,作出表示正弦值的有向线段,得到正弦线的概念.(2)由学生仿照正弦线,得到余弦线.11OxyMP角的终边。。。。。。ACB.有向线段分别叫做角的正弦线、余弦线.小结:我们已经得到角的正弦线、余弦线、正切线,它们都是与单位圆的弦有关的线段.3.正切线(1)探索讨论问题 9:能不能用有向线段表示角的正切呢?问题 10:正切函数值是怎样定义的?怎样才能简化定义中的表达式?这个表达式和正弦函数值的表达式有什么不同?怎样才能...