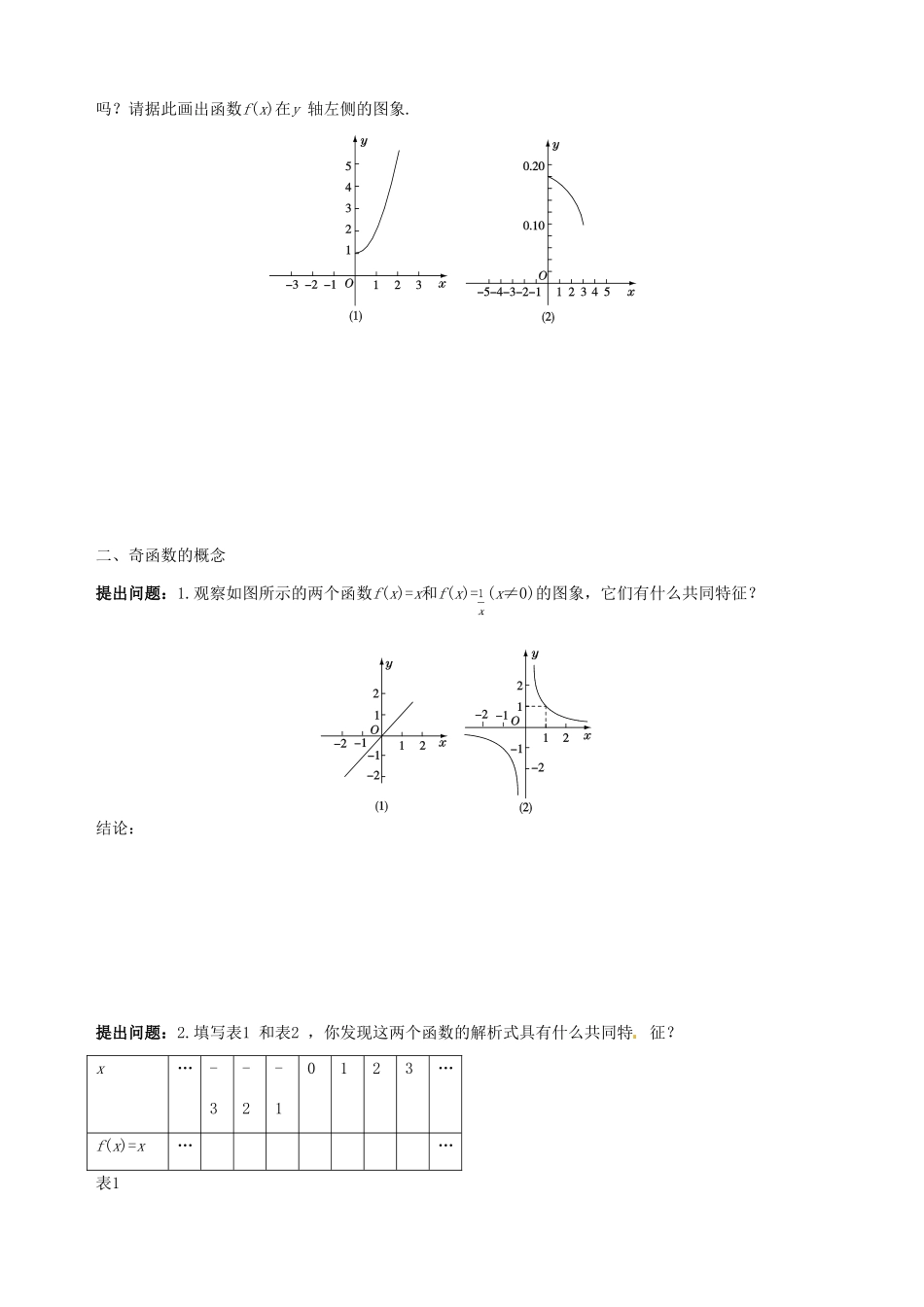
第 1 课 时 函 数 的 奇 偶 性1.理解函数奇偶性的含义,会判断一些函数的奇偶性.2.掌握偶函数的图象关于 y 轴对称,奇函数的图象关于原点对称的特性.1.一般地,如果对于函数f(x)的 x ,都有 ,那么函数f(x)就叫做偶函数. 一般地,对于函数f(x)的 x ,都有 ,那么函数f(x)就叫做奇函数.2.偶函数的图象关于 对称,奇函数的图象关于 对称.3.若奇函数f(x)的定义域中含有0 ,则必有f(0)= .1.(2013·山东高考)已知函数 f(x)为奇函数,且当 x>0 时,+ ,则 f(-1)=( )A.2 B.1 C.0 D.-22.函数f(x)= -x的图象关于( )A.y 轴对称 B.直线y=-x对称C.坐标原点对称 D . 直线y=x 对称3.函数f(x)=( )A.是奇函数B.是偶函数C.既不是偶函数也不是奇函数D.是既奇又偶函数4.(2012· 重庆高考) 若f(x)=(x+a)(x-4) 为偶函数,则实数a= .一、偶函数的概念提出问题:1.请同学们思考一下,初中我们学习的轴对称图形与中心对称图形的概念是什么?结论:提出问题:2.观察如图所示的两个函数和f(x)=2-|x|的图象,它们有什么共同特征? (1) (2)结论:提出问题: 3.对两个函数,我们分别计算几个特殊的函数值: f (-3),f (3 ),f (-2 ),f (2 ),f (-1), f (1 ),观察并猜想,它们有何关系?结论:提出问题:4 :如和f(x)=2-|x|这类的函数,当自变量x 取一对相反数时,相应的两个函数值相同,称这样的函数为偶函数. 你能给出偶函数的定义吗?结论:反馈练习1 如图 (1) 和(2) 分别是+1和f(x)=图象的一部分,这两个函数是偶函数吗?请据此画出函数f(x)在y 轴左侧的图象.二、奇函数的概念提出问题:1.观察如图所示的两个函数f(x)=x和f(x)= (x≠0)的图象,它们有什么共同特征?结论:提出问题:2.填写表1 和表2 ,你发现这两个函数的解析式具有什么共同特征?x…-3-2-10123…f(x)=x……表1x…-3-2-10123…f(x)=…Ï…表2结论:提出问题:3.与偶函数的定义类似,像f(x)=x和f(x)= (x≠0)这类的函数,当自变量x 取一对相反数时,相应的两个函数值也是一对相反数,称这样的函数为奇函数. 你能给出奇函数的定义吗?结论:提出问题:4.若任意一个奇函数f(x)在原点处有定义,f(0)是定值吗?结论:反馈练习2 已知函数+2x 是奇函数,则实数a= .三、函数奇偶性的判断提出问题:1.函数,x∈ [-2,2)是偶函数吗?为什么?结论:提出问题:2.由问题1 ,结合偶函数的定义,偶函数的定义域有什么特点?...