【四维备课】高中数学 1.5《函数y=Asin(ωx+φ)的图象》教学设计 新人教A版必修4

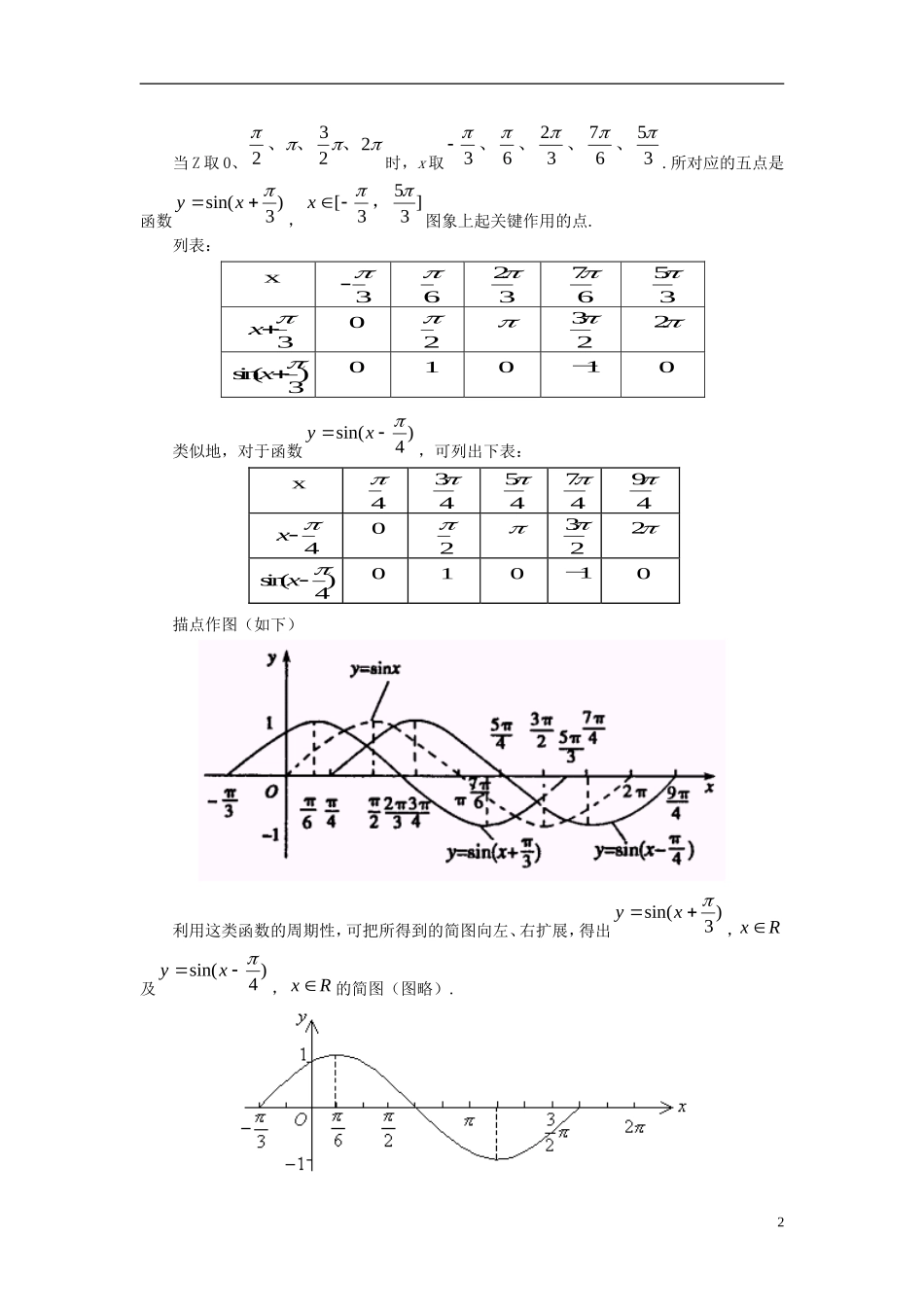
yxsin()31.5《函数的图象》教学设计【教学目标】1.通过五点作图法正确找出函数 y＝sin x 到 y＝sin(ωx+φ)的图象变换规律.2.对“周期变换、相位变换先后顺序调整后，将影响图象平移量”的理解．3.会用“五点法”作出函数以及函数的图象. 4.能说出对函数的图象的影响. 5.能够将的图象变换到的图象，并会根据条件求解析式.【导入新课】复习引入：在现实生活中，我们常常会遇到形如 y＝Asin(ωx＋ )的函数解析式(其中A，ω， 都是常数)，下面我们讨论函数 y＝Asin(ωx＋ )，x∈R 的简图的画法.1．正弦曲线-11yx-6-565-4-3-2-0432f x  = sin x 2.余弦曲线-11yx-6-565-4-3-2-0432f x  = cos x 3.五点法作图新授课阶段1．函数图象的左右平移变换 如在同一坐标系下，作出函数和的简图，并指出它们与 yxsin图象之间的关系. 解 析 ： 函数的周期为 2 ，我们来作这个函数在长度为一个周期的闭区间上的简图.设xZ3，那么，xZ 3sin()sinxZ31yxsin()4yxsin()3 当 Z 取 0、2322、 、、时，x 取 36237653、、、、.所对应的五点是函数yxsin()3 ，x  []353，图象上起关键作用的点. 列表：x 3 6 23 76 53 x3 0 2  32 2 sin()x3 0 1 0 －1 0 类似地，对于函数yxsin()4，可列出下表：x 4 34 54 74 94 x 4 0 2  32 2 sin()x 4 0 1 0 －1 0 描点作图（如下） 利用这类函数的周期性，可把所得到的简图向左、右扩展，得出yxsin()3 ，xR及yxsin()4， xR的简图（图略）.2 由图可以看出，yxsin()3 的图象可以看做是把 yxsin的图象上所有的点向左平行移动3 个单位而得到的， yxsin()4的图象可以看做是把 yxsin的图象上所有的点向右平行移动4 个单位得到的. 注意：一般地，函数 yxsin()() 0 的图象，可以看做是把 yxsin的图象上所有的点向左（当  0 时）或向右（当  0 时）平行移动| | 个单位而得到的.例 1 画出函数 y＝sin(x＋)，x∈R，y＝sin(x－)，x∈R 的简图.解：列表x-x+02sin(x+)010–10描点画图：xx－02sin(x–)010–10通过比较，发现：3(1)函数 y＝sin(x＋)，x∈R 的图象可看...