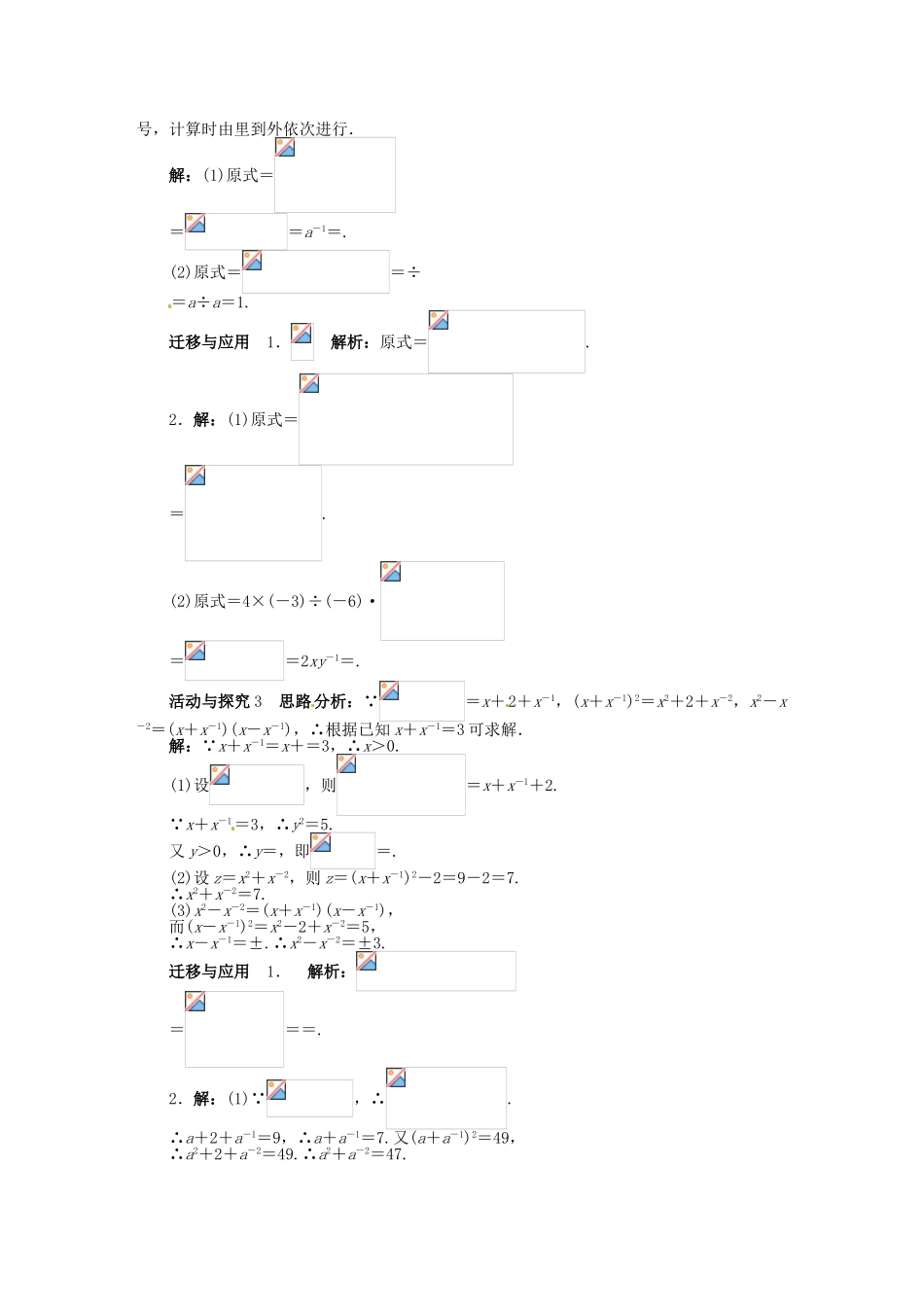
第 2 课时 指数幂的运算问题导学一、利用有理指数幂的性质求值活动与探究 1化简下列各式(其中字母均表示正数):(1)-0++16-0.75+;(2).迁移与应用计算下列各式:(1)0.5+0.1-2+-3π0+;(2)--1×-10×;(3)(x>0,y>0);(4).若幂的底数是带分数,则先化为假分数,若底数能写成幂的形式,就先将其写成幂的形式,然后再按运算顺序进行计算.二、根式与分数指数幂的综合运算活动与探究 2(1)(a>0,b>0);(2)÷(a>0).迁移与应用1.(a>0)=____.2.化简下列各式:(1);(2)4·(-3)·÷.在进行根式与分数指数幂的混合运算时,先把根式化为分数指数幂,再运用有理指数幂的运算性质进行化简求值.遇到多重根号时,应由里到外写成分数指数幂再进行运算.三、条件化简求值活动与探究 3已知 x+x-1=3,求下列各式的值:(1);(2)x2+x-2;(3)x2-x-2.迁移与应用1.若 a m=2,an=3,则=______.2.(1)已知,求 a2+a-2的值;(2)已知+b=1,求的值.解答 条件求值与化简问题时,要认真分析条件与所求式之间的联系,进而找到解答问题的思路与方法.当堂检测1.下列运算正确的是( )A.a·a2=a2 B.(ab)3=ab3C.(a2)3=a6 D.a10÷a2=a52.下列运算结果中正确的为( )A.a2·a3=a6 B.(-a2)3=(-a3)2C.(-1)0=1 D.(-a2)3=-a63.化简(a>0,b>0)的结果是( )A. B.C. D.4.计算:=______.5.若 10x=3,10y=4,则 102x-y=______.提示:用最精炼的语言把你当堂掌握的核心知识的精华部分和基本技能的要领部分写下来并进行识记.答案:课前预习导学【预习导引】1.(1)ar+s (2)ars (3)arbr预习交流 1 (1)提示:有理指数幂的运算性质是整数指数幂的运算性质的推广.(2) a4b92.实数 有理数指数幂课堂合作探究【问题导学】活动与探究 1 思路分析:若幂的底数能写成幂的形式,就先写成幂的形式,再利用有理指数幂的运算性质,先乘方,再乘除,最后加减.解:(1)原式=-1+(-2)-4+2-3+=(0.4)-1-1+++0.1=.(2)原式=[2×(-6)÷(-3)]=4ab0=4a.迁移与应用 解:(1)原式=+-2+-3+=+100+-3+=100.(2)原式=-(3×1)-1×-10×=-×1-3=0.(3)原式=.(4)原式=[4×(-3)÷(-6)]=.活动与探究 2 思路分析:(1)先将根式化为分数指数幂,再进行运算;(2)中有多重根号,计算时由里到外依次进行.解:(1)原式===a-1=.(2)原式==÷=a÷a=1.迁移与应用 1. 解析:原式...