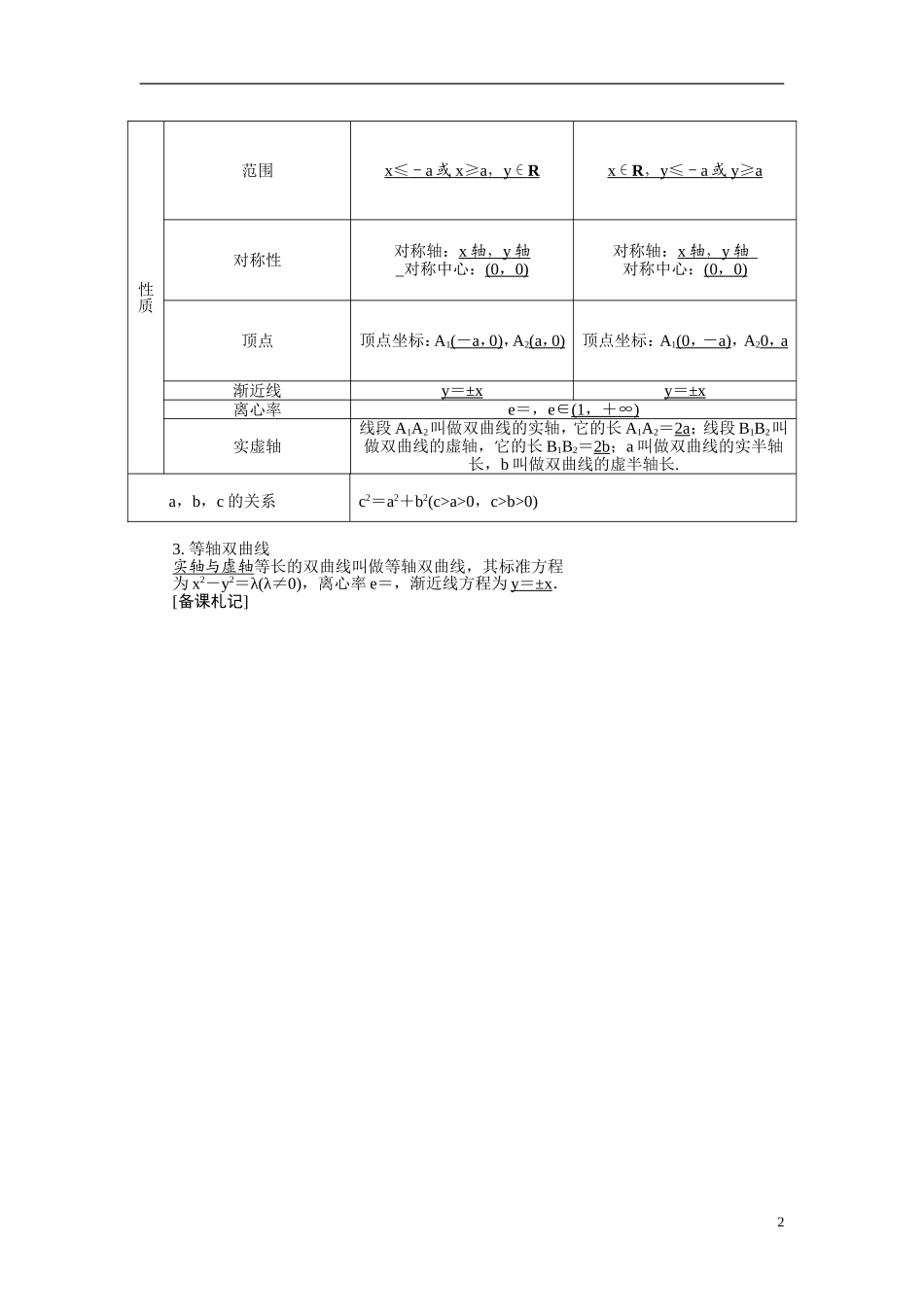
第九章平面解析几何第 8 课时 双 曲 线第十章考情分析考点新知建立并掌握双曲线的标准方程,能根据已知条件求双曲线的标准方程;掌握双曲线的简单几何性质,能运用双曲线的几何性质处理一些简单的实际问题.① 了解双曲线的定义、几何图形和标准方程,知道它们的简单几何性质.② 掌握双曲线的简单应用.1. 若双曲线方程为 x2-2y2=1,则它的左焦点的坐标为________.答案:解析: 双曲线方程可化为 x2-=1,∴ a2=1,b2=.∴ c2=a2+b2=,c=.∴ 左焦点坐标为.2. 双曲线-=1 的渐近线方程为________.答案:y=±2x解析: a=2,b=4,∴ 双曲线的渐近线方程为 y=±2x.3. 若双曲线-y2=1 的一个焦点为(2,0),则它的离心率为________.答案:解析:依题意得 a2+1=4,a2=3,故 e===.4. (选修 11P39习题 2(2)改编)双曲线的焦点在 x 轴上,虚轴长为 12,离心率为,则双曲线的标准方程为______________________. 答案:-=1解析:焦点在 x 轴上,设所求双曲线的方程为-=1.由题意,得解得∴ 焦点在 x 轴上的双曲线方程为-=1.5. 设 F1,F2是双曲线 x2-=1 的两个焦点,P 是双曲线上的一点,且 3PF1=4PF2,则△PF1F2的面积等于________.答案:24解析:由 P 是双曲线上的一点和 3PF1=4PF2可知,PF1-PF2=2,解得 PF1=8,PF2=6.又F1F2=2c=10,所以△PF1F2为直角三角形,所以△PF1F2的面积 S=×6×8=24.1. 双曲线的定义平面内到两个定点 F1,F2的距离的差的绝对值等于常数(小于 F1F2的正数)的点的轨迹叫做双曲线,这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.2. 双曲线的标准方程和几何性质标准方程-=1(a>0,b>0)-=1(a>0,b>0)图形1性质范围x ≤ - a 或 x ≥ a , y ∈ R x ∈ R , y ≤ - a 或 y ≥ a 对称性对称轴:x 轴 , y 轴 _对称中心:(0 , 0 ) 对称轴:x 轴 , y 轴 _对称中心:(0 , 0 ) 顶点顶点坐标:A1( - a , 0 ) ,A2(a , 0 ) 顶点坐标:A1(0 , - a) ,A20 , a 渐近线y = ± x y = ± x 离心率e=,e∈(1 , + ∞ ) 实虚轴线段 A1A2叫做双曲线的实轴,它的长 A1A2=2a;线段 B1B2叫做双曲线的虚轴,它的长 B1B2=2b;a 叫做双曲线的实半轴长,b 叫做双曲线的虚半轴长.a,b,c 的关系c2=a2+b2(c>a>0,c>b>0)3. 等轴双曲线实轴与虚...