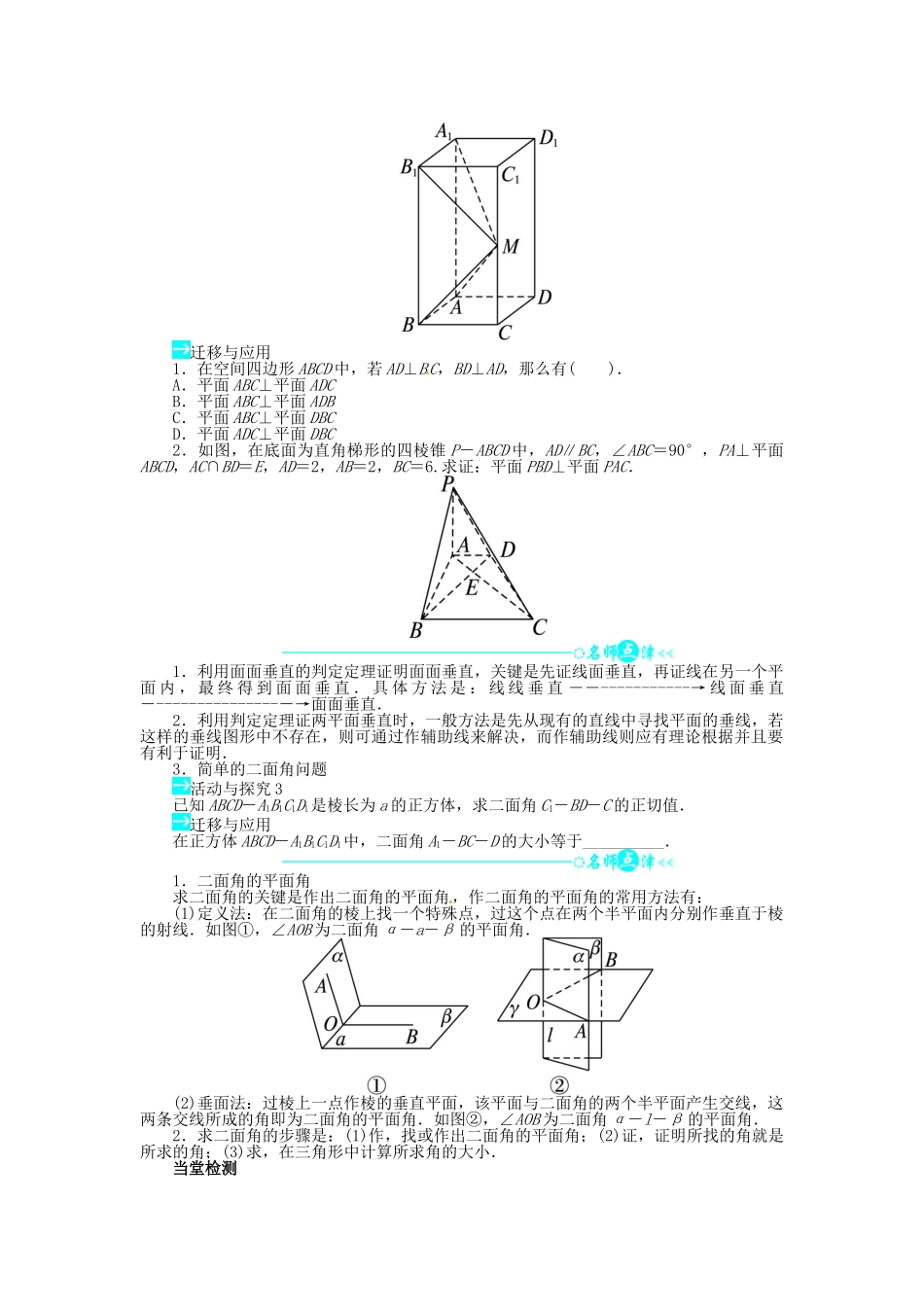
§6 垂直关系6.1 垂直关系的判定问题导学1.线面垂直的判定活动与探究 1如图,在三棱锥 P-ABC 中,PA⊥平面 ABC,∠ABC=90°,在平面 PAB 中,作 AH⊥PB.(1)求证:BC⊥平面 PAB;(2)求证:AH⊥平面 PBC.迁移与应用1.已知四棱锥 P-ABCD 的底面是菱形,且∠ABC=60°,PA=PC=2,PB=PD.若 O 是AC 与 BD 的交点,求证:PO⊥平面 ABCD.2.在空间四边形 ABCD 中,若 AB=AC,DB=DC,求证:BC⊥AD.1.利用直线和平面垂直的判定定理证明直线与平面垂直的步骤:(1)在这个平面内找两条直线,证明它和这条直线垂直;(2)说明这个平面内的两条直线是相交的直线;(3)根据判定定理得出结论.2.利用直线和平面垂直的判定定理判定直线与平面垂直的技巧:证明线面垂直的关键是分析几何图形,寻找隐含的和题目中推导出的线线垂直关系,进而证明线面垂直.三角形全等、等腰三角形底边的中线、梯形的高、菱形、正方形的对角线、三角形中的勾股定理等都是找线线垂直的方法.3.证明线面垂直时,需要先证线线垂直,而线线垂直关系的获得往往是先证得线面垂直,从而根据线面垂直的定义得出线线垂直,因此证明过程通常是反复利用线面垂直的定义及线面垂直判定定理的过程.2.面面垂直的判定活动与探究 2如图所示,在长方体 ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M 是棱 CC1的中点.求证:平面 ABM⊥平面 A1B1M.迁移与应用1.在空间四边形 ABCD 中,若 AD⊥BC,BD⊥AD,那么有( ).A.平面 ABC⊥平面 ADCB.平面 ABC⊥平面 ADBC.平面 ABC⊥平面 DBCD.平面 ADC⊥平面 DBC2.如图,在底面为直角梯形的四棱锥 P-ABCD 中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,AC∩BD=E,AD=2,AB=2,BC=6.求证:平面 PBD⊥平面 PAC.1.利用面面垂直的判定定理证明面面垂直,关键是先证线面垂直,再证线在另一个平面 内 , 最 终 得 到 面 面 垂 直 . 具 体 方 法 是 : 线 线 垂 直 ――-----------→ 线 面 垂 直―---------------―→面面垂直.2.利用判定定理证两平面垂直时,一般方法是先从现有的直线中寻找平面的垂线,若这样的垂线图形中不存在,则可通过作辅助线来解决,而作辅助线则应有理论根据并且要有利于证明.3.简单的二面角问题活动与探究 3已知 ABCD-A1B1C1D1是棱长为 a 的正方体,求二面角 C1-BD-C 的正切值.迁移与应用在正方体 ABCD-A1B1C1D1中,二面角 A1-BC-D ...