【课堂新坐标】（教师用书）2013-2014学年高中数学 1.2 平行线分线段成比例定理教案 新人教A版选修4-1

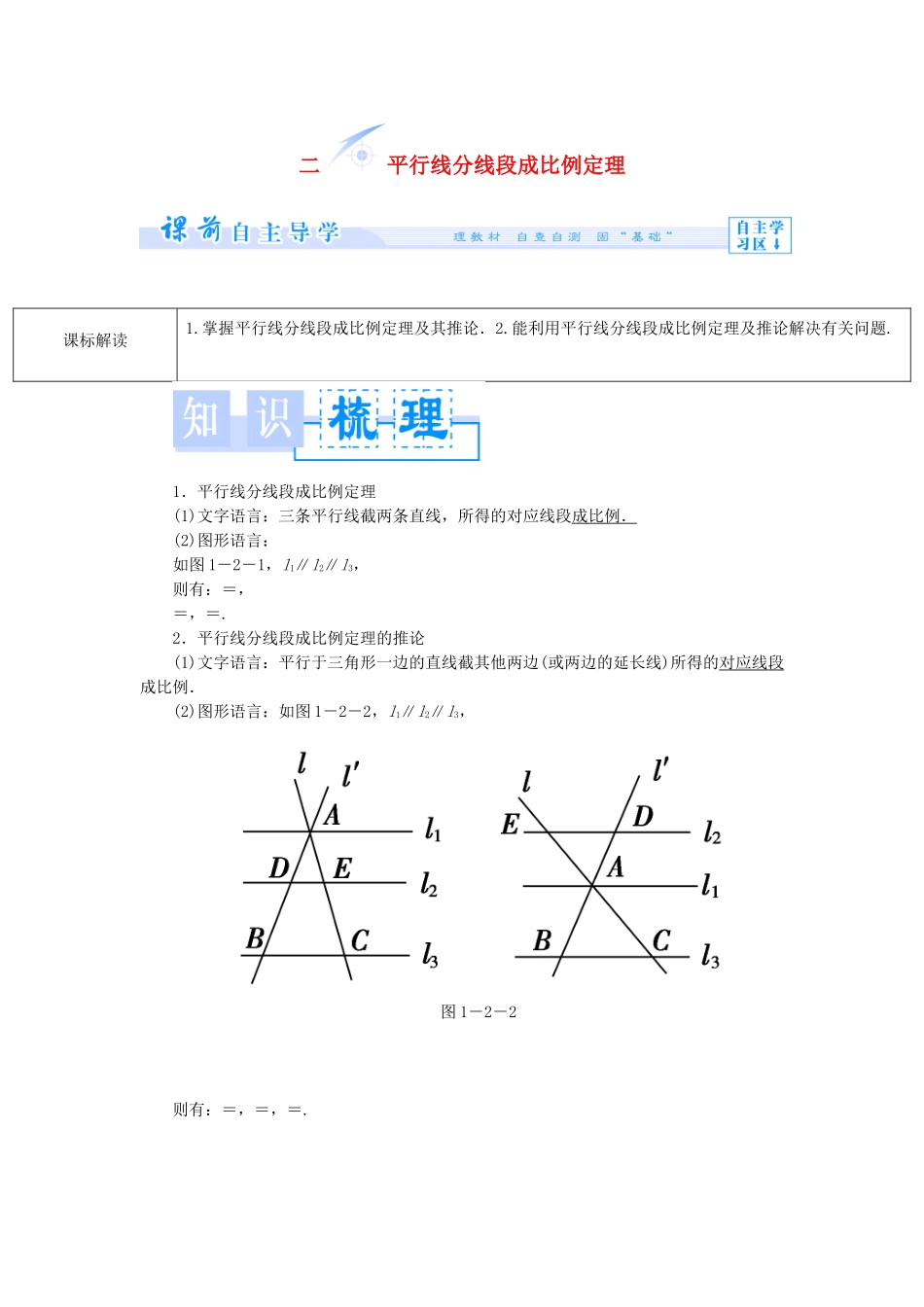
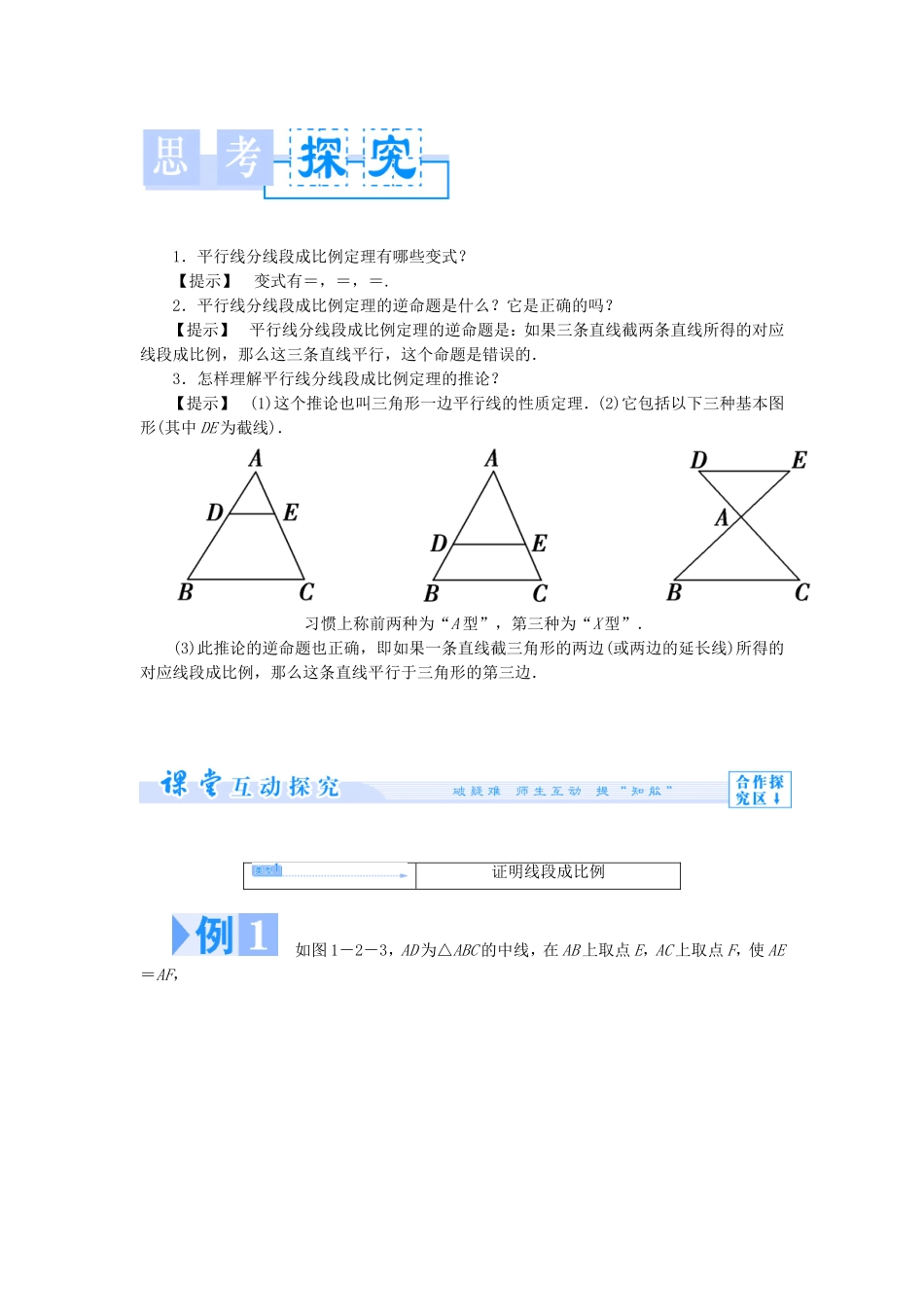
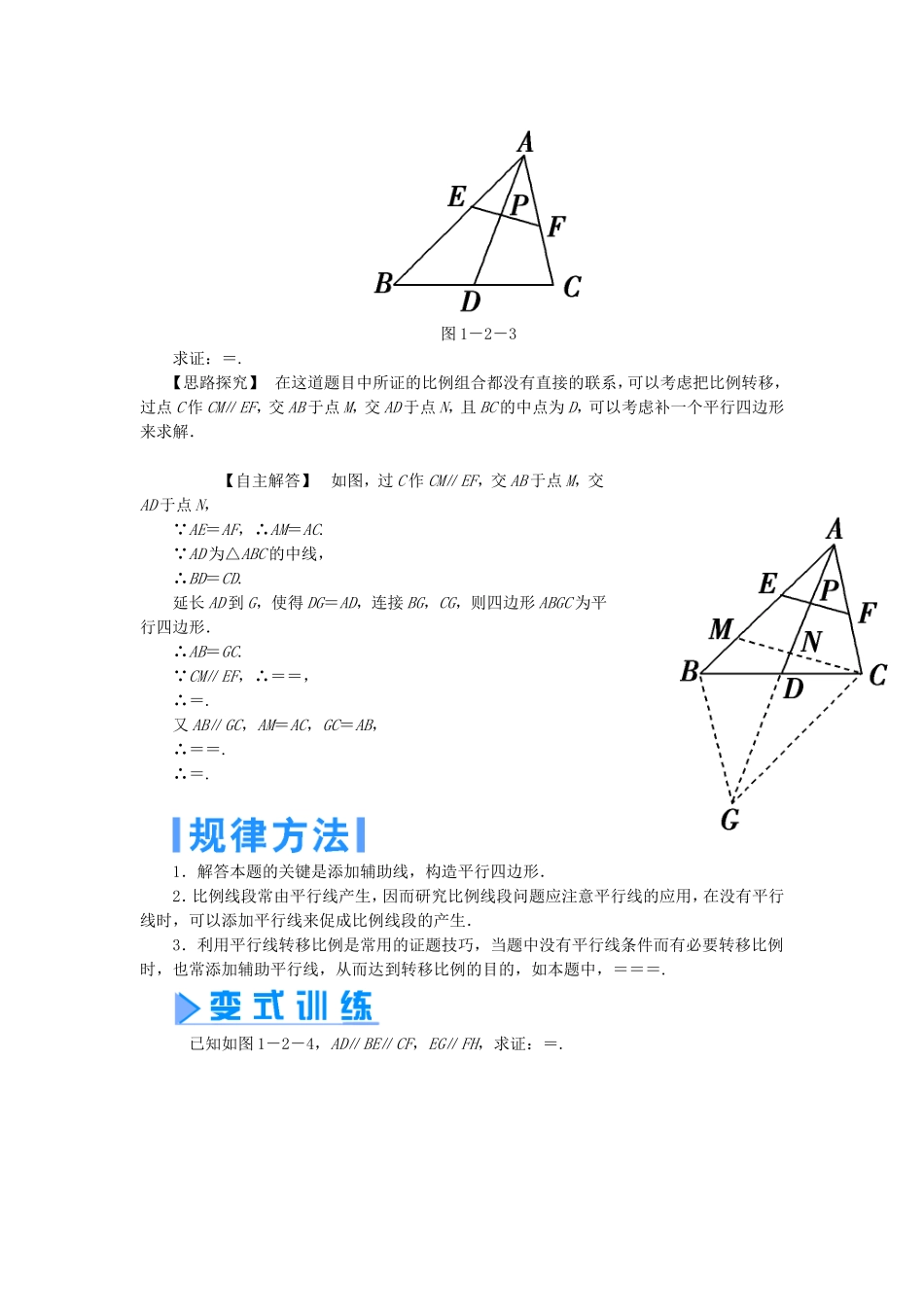
二平行线分线段成比例定理课标解读1.掌握平行线分线段成比例定理及其推论．2.能利用平行线分线段成比例定理及推论解决有关问题.1．平行线分线段成比例定理(1)文字语言：三条平行线截两条直线，所得的对应线段成比例．(2)图形语言：如图 1－2－1，l1∥l2∥l3，则有：＝，＝，＝.2．平行线分线段成比例定理的推论(1)文字语言：平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例．(2)图形语言：如图 1－2－2，l1∥l2∥l3，图 1－2－2则有：＝，＝，＝.1．平行线分线段成比例定理有哪些变式？【提示】 变式有＝，＝，＝.2．平行线分线段成比例定理的逆命题是什么？它是正确的吗？【提示】 平行线分线段成比例定理的逆命题是：如果三条直线截两条直线所得的对应线段成比例，那么这三条直线平行，这个命题是错误的．3．怎样理解平行线分线段成比例定理的推论？【提示】 (1)这个推论也叫三角形一边平行线的性质定理．(2)它包括以下三种基本图形(其中 DE 为截线)．习惯上称前两种为“A 型”，第三种为“X 型”．(3)此推论的逆命题也正确，即如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例，那么这条直线平行于三角形的第三边．证明线段成比例 如图 1－2－3，AD 为△ABC 的中线，在 AB 上取点 E，AC 上取点 F，使 AE＝AF，图 1－2－3求证：＝.【思路探究】 在这道题目中所证的比例组合都没有直接的联系，可以考虑把比例转移，过点 C 作 CM∥EF，交 AB 于点 M，交 AD 于点 N，且 BC 的中点为 D，可以考虑补一个平行四边形来求解．【自主解答】 如图，过 C 作 CM∥EF，交 AB 于点 M，交AD 于点 N， AE＝AF，∴AM＝AC. AD 为△ABC 的中线，∴BD＝CD.延长 AD 到 G，使得 DG＝AD，连接 BG，CG，则四边形 ABGC 为平行四边形．∴AB＝GC. CM∥EF，∴＝＝，∴＝.又 AB∥GC，AM＝AC，GC＝AB，∴＝＝.∴＝.1．解答本题的关键是添加辅助线，构造平行四边形．2．比例线段常由平行线产生，因而研究比例线段问题应注意平行线的应用，在没有平行线时，可以添加平行线来促成比例线段的产生．3．利用平行线转移比例是常用的证题技巧，当题中没有平行线条件而有必要转移比例时，也常添加辅助平行线，从而达到转移比例的目的，如本题中，＝＝＝. 已知如图 1－2－4，AD∥BE∥CF，EG∥FH，求证：＝.图 1－2－4【证明】 AD∥BE∥CF，∴＝，又 EG∥FH，∴＝，∴＝.证明线段...