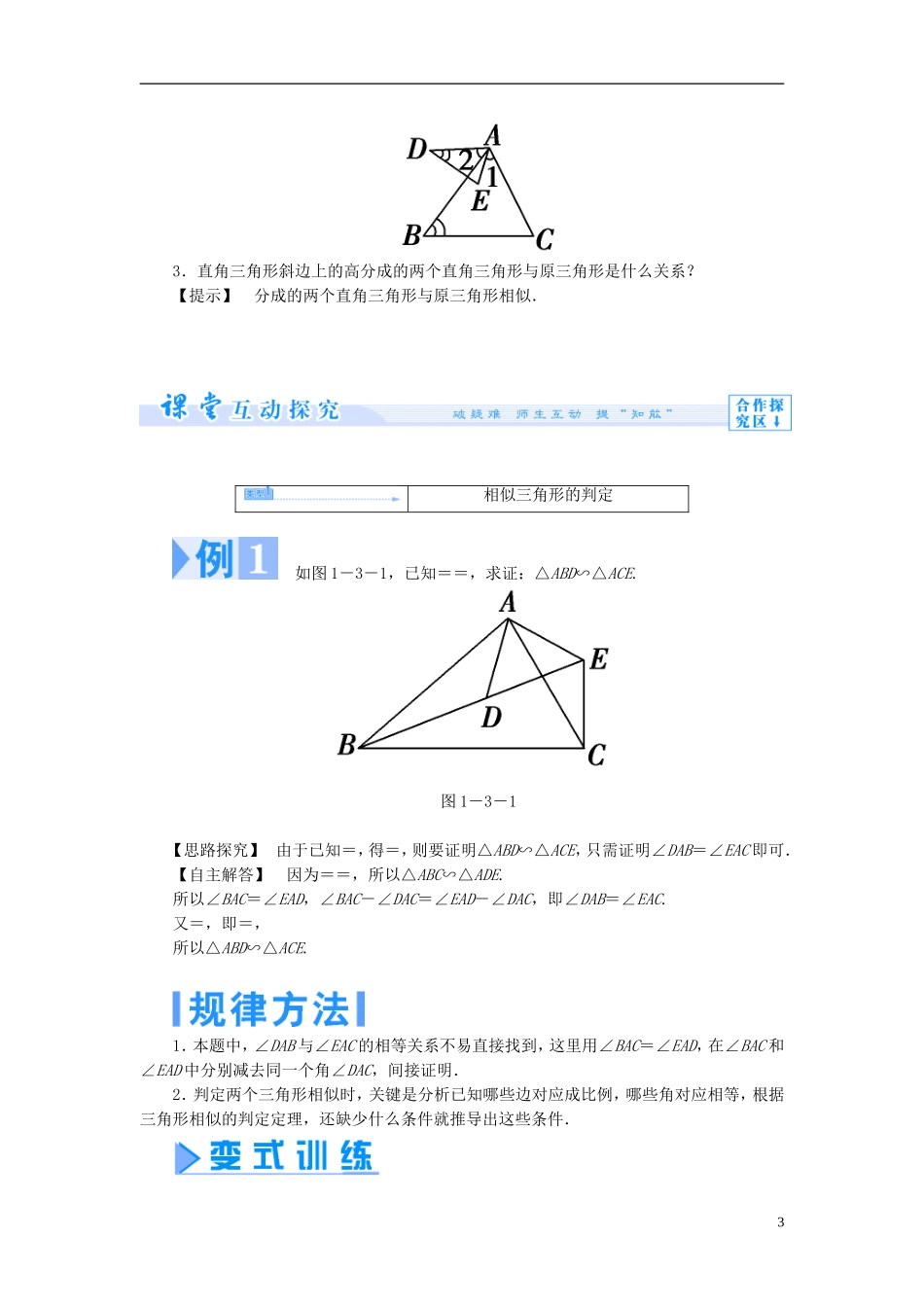
三相似三角形的判定及性质1 相似三角形的判定课标解读1.了解三角形相似的定义.2.掌握相似三角形的判定定理,以及直角三角形相似的判定方法.1.相似三角形的有关概念(1)定义:对应角相等,对应边成比例的两个三角形叫做相似三角形.(2)相似比:相似三角形对应边的比值叫做相似比(或相似系数).2.预备定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.3.相似三角形的判定定理名称定理内容简述判定定理 1对于任意两个三角形,如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.两角对应相等,两三角形相似判定定理 2对于任意两个三角形,如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.两边对应成比例且夹角相等,两三角形相似.判定定理 3对于任意两个三角形,如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.三边对应成比例,两三角形相似.4.引理1如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.5.直角三角形相似的判定(1)上述所有的任意三角形相似的判定适用于直角三角形.(2)定理 1:如果两个直角三角形有一个锐角对应相等,那么它们相似.(3)定理 2:如果两个直角三角形的两条直角边对应成比例,那么它们相似.(4)定理 3:如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.1.用符号表示相似三角形时,应注意哪些问题?【提示】 (1)用符号表示相似三角形时,在两个相似三角形中,三边对应成比例,即==,每个比的前项是同一个三角形的三条边,而比的后项分别是另一个三角形的对应边,它们的位置不能写错.(2)用符号表示相似三角形时,对应顶点的字母写在对应的位置上,这样可以很快地找到相似三角形的对应角或对应边.如若△ABC∽△DEF,则∠A=∠D,∠B=∠E,∠C=∠F,==.2.三角形相似的判定定理一是最常用的判断方法,使用此判定方法解题的常用基本图形有哪几种?【提示】 (1)平行线型:(2)相交线型:(3)旋转型:23.直角三角形斜边上的高分成的两个直角三角形与原三角形是什么关系?【提示】 分成的两个直角三角形与原三角形相似.相似三角形的判定 如图 1-3-1,已知==,求证:△ABD∽△ACE.图 1-3-1【思路探究】 由于已知=,得=,则要...