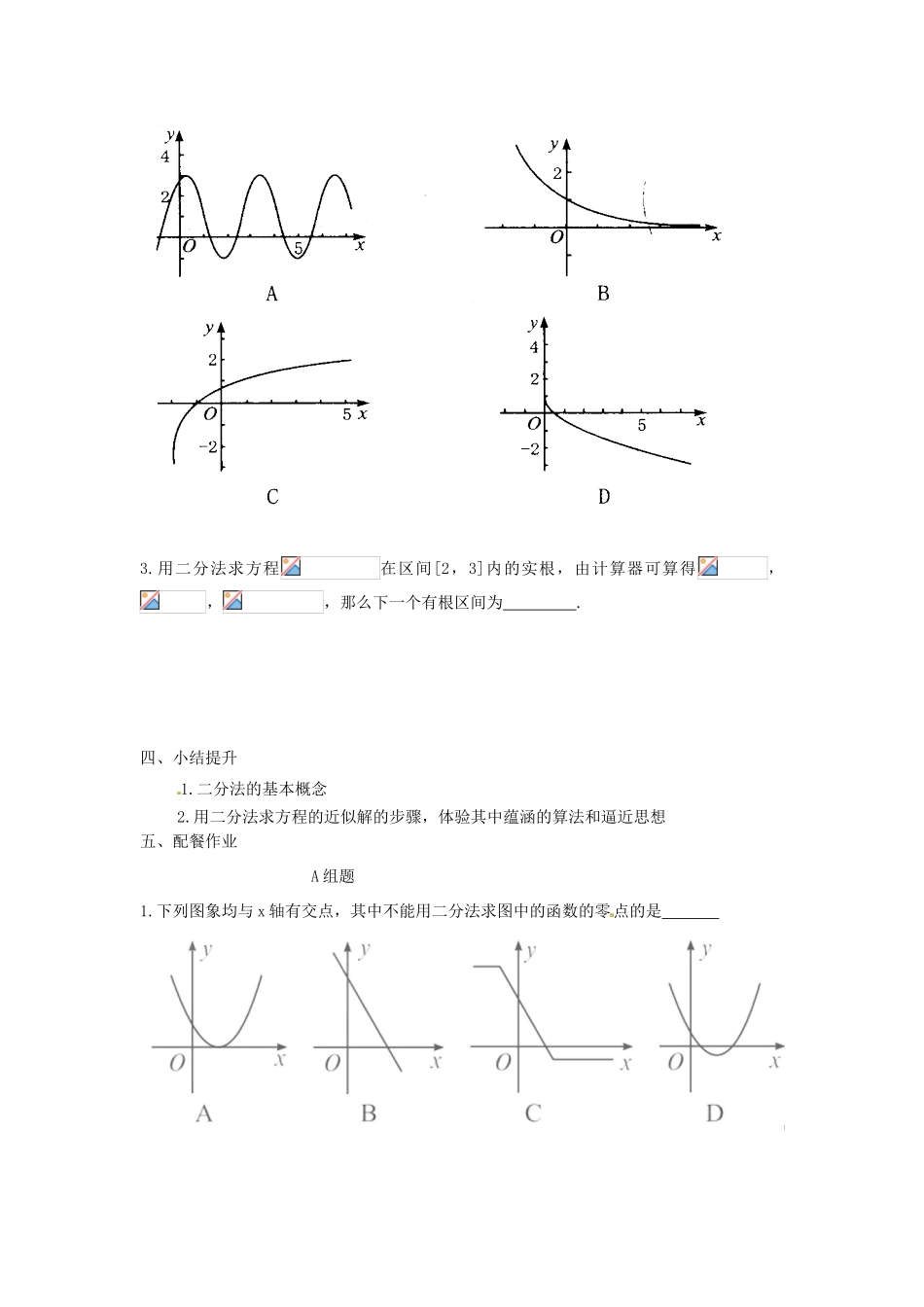
云南省德宏州梁河县一中高中数学必修一:3.1.2 用二分法求方程的近似解(学案)班级 姓名 学号 一、前置作业(预习教材 P89~ P91,找出疑惑之处)复习 1:什么叫零点?零点的等价性?零点存在性定理?对于函数,我们把使 的实数 x 叫做函数的零点.方程有实数根函数的图象与 x 轴 函数 .如果函数在区间上的图象是连续不断的一条曲线,并且有 ,那么,函数在区间内有零点.二、教学内容与例题(一)、内容问题 1:求方程的根,可以选用哪些方法?问题 2:是否所有的方程都可以选用以上的三种方法来求它的根?问题 3:如何求方程的根?问题 4: 从城市 A 到城市 B 的供电线路的某一处发生了故障,已知这条线路的长度是 10Km,每 50m 有一根电线杆,如何迅速查出故障的所在位置? 问题 5:如何设计最佳方案查找故障点所在的范围?(二分法)答案一:把线路分成很多小段,一段一段的去检验,最终可以找出故障点所在的线路范围由此得到:此方法尽管自然,但效率较低,无规律可循,也不便实际应用.答案二:直接将故障点所在区间范围不断分成两部分,逐步缩小检验范围,最终看故障点在哪个部分,这种方法是我们所期待的,在此基础上引出方案中最简单的一种:二分,从而引出二分法思想.二分法:对于在区间上连续不断且的函数,通过不断地把函数的零点所在区间一分为二,使区间的两个端点逐步逼近零点,从而得到零点的近似值的方法叫做二分法给定精确度,用二分法求函数零点近似值的步骤如下:(1)确定区间,验证,给精确度;(2)求区间的中点;(3)计算;① 若,则 c 就是函数的零点;② 若,则令(此时零点);③ 若,则令(此时零点).(二)、例 1 借助计算器或计算机,利用二分法求方程的近似解.三、目标检测1. 若函数在区间上为减函数,则在上( ).A. 至少有一个零点 B. 只有一个零点C. 没有零点 D. 至多有一个零点2. 下列函数图象与轴均有交点,其中不能用二分法求函数零点近似值的是( ).3.用二分法求方程在区间[2,3]内的实根,由计算器可算得,,,那么下一个有根区间为 .四、小结提升1.二分法的基本概念2.用二分法求方程的近似解的步骤,体验其中蕴涵的算法和逼近思想五、配餐作业A 组题1.下列图象均与 x 轴有交点,其中不能用二分法求图中的函数的零点的是 2.已知函数的图象是连续不断的,且有如下对应值表:1234564 1.306 -1.098 7.386-5.6097.791函数在那几个区间有零点?为什么?3. 函数的零点所在区间为( ). A. B. C. D. B 组题4. 函数的零点个数为 ,大致所在区间为 .