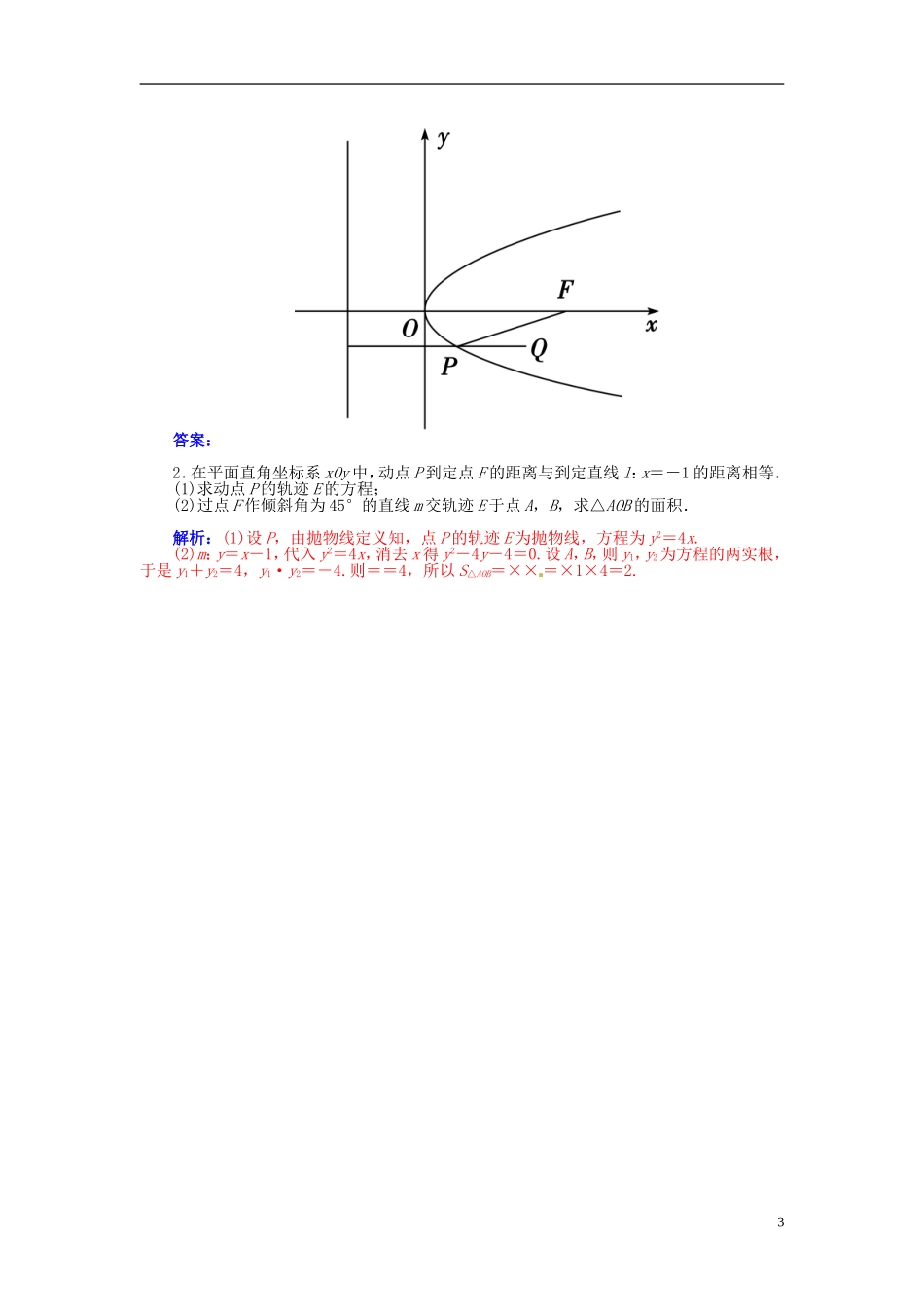
第九节 抛物线(一)知识梳理一、抛物线的定义平面内到定点 F 的距离等于到定直线 l(定点不在定直线上)的距离的点的轨迹是抛物线.其中定点叫做焦点,定直线叫做准线.注意:当定点在定直线上时,点的轨迹是过该定点且与定直线垂直的一 条直线.二、抛物线的类型、标准方程及其几何性质(注意:表中各式的 p>0)标准方程y2=2pxy2=-2pxx2=2pyx2=-2py图形焦点FFFF准线x=-x=y=-y=范围x≥0,y∈Rx≤0,y∈Rx∈R,y≥0x∈R,y≤0对称轴x 轴y 轴顶点(0,0)离心率e=1焦半径 = + x1 = + = + y1 = + 基础自测1.已知抛物线 y2=2px 上一点 M(1,m)到其焦点的距离为 5,则该抛物线的准线方程为( )A.x=8 B.x=-8 C.x=4 D.x=-4解析:由题意得 1+=5,故 p=8,所以准线方程为 x=-=-4,故选 D.答案:D2.一动圆的圆心在抛物线 x2=-8y 上,且动圆恒与直线 y-2=0 相切,则动圆必过定点( )A.(4,0) B.(0,-4) C.(2,0) D.(0,-2)解析:由抛物线的定义知到焦点距离与到准线的距离相等,动圆必过焦点(0,-2).故选D.答案:D3.若动点 P 到点 F(2,0)的距离与它到直线 x+2=0 的距离相等,则点 P 的轨迹方程为____________.解析:由抛物线定义知点,P 的轨迹是以 F(2,0)为焦点,直线 x=-2 为准线的抛物线,所以 p=4,所以其方程为 y2=8x.11.掌握抛物线的定义、几何图形、标准方程及简单性质.2.理解数形结合的思想.答案:y2=8x4.若抛物线 y2=2px 的焦点与椭圆 +=1 的右焦点重合,则 p 的值为________.解析:椭圆+=1 的右焦点为(2,0),所以抛物线 y2=2px 的焦点为(2,0),则 p=4.答案:4 1.(2013·四川卷)抛物线 y2=4x 的焦点 F(1,0)到双曲线 x2-=1 的渐近线的距离是( )A. B. C.1 D.解析:抛物线 y2=4x 的焦点 F(1,0),双曲线 x2-=1 的渐近线是 y=±x,即 x±y=0,所以所求距离为= .故选 B.答案:B2.已知平面内一动点 P 到点 F(1,0)的距离与点 P 到 y 轴的距离的差等于 1.(1)求动点 P 的轨迹 C 的方程;(2)过点 F 作两条斜率存在且互相垂直的直线 l1,l2,设 l1与轨迹 C 相交于点 A,B,l2与轨迹 C 相交于点 D,E,求 AD·EB的最小值.解析:(1)设动点 P 的坐标为(x,y),由题意有-|x|=1.化简得 y2=2x+2|x|.当 x≥0 时,y2=4x;当 x<0 时,y=0.所以,动点 P 的轨迹 C 的...