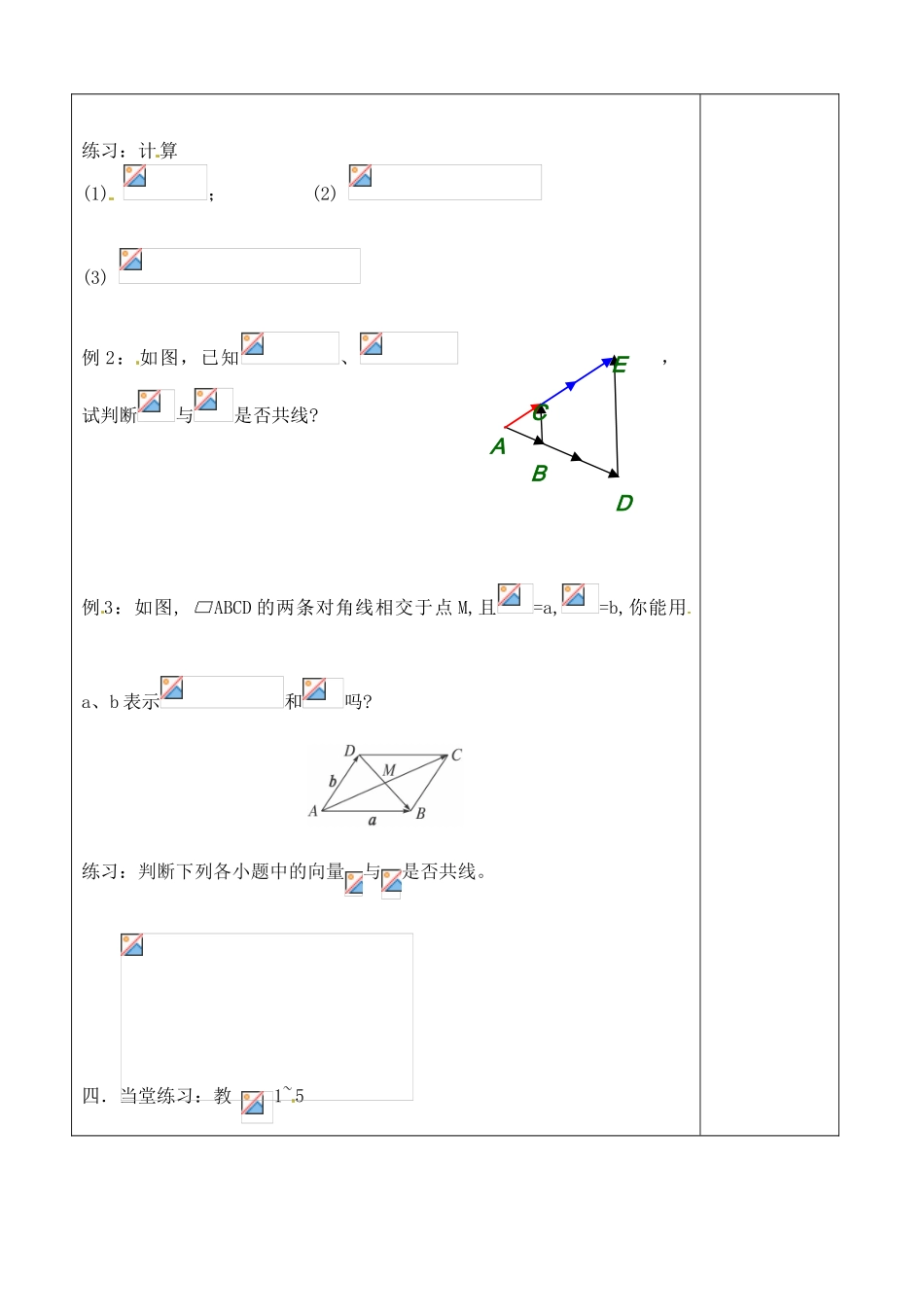
吉林省吉林市朝鲜族中学 2014 高中数学 2.2.3 向量数乘运算及其几何意义学案(无答案)新人教 A 版必修 4学习目标1、掌握实数与向量积的定义,理解实数与向量 积的几何意义;2、掌握实数与向量的积的运算律;3、理解向量共线定理,能够运用定理解决共线等问题。学习重点理解实数与向量积的几何意义学习难点向量共线定理及应用 学 习 内 容学法指导一.知识点1.向量的数乘定义:实数 λ 与向量的积是一个 ,记作: 。其大小和方向规定如下:① 大小:② 方向:λ>0 时,与方向相同;λ<0 时,与方向相反。特别地,当或时。2.运算律:设、为任意向量,、为任意实数,则有:① 结合律: ② 第一分配律:③ 第二分配律: 3. 向量共线定理 : 向量与非零向量共线当且仅当有唯一一个实数,使得 。三.典型例题例 1: 向 量 的 加 、减、数乘运算统称为向量的线性运算。运算律的应用共线定理的应用练习:计算(1) ; (2) (3) 例 2: 如图,已知、,试判断与是否共线?例 3:如图, ABCD 的两条对角线相交于点 M,且=a,=b,你能用a、b 表示和吗?练习:判断下列各小题中的向量与是否共线。四.当堂练习:教 1~5CEABD