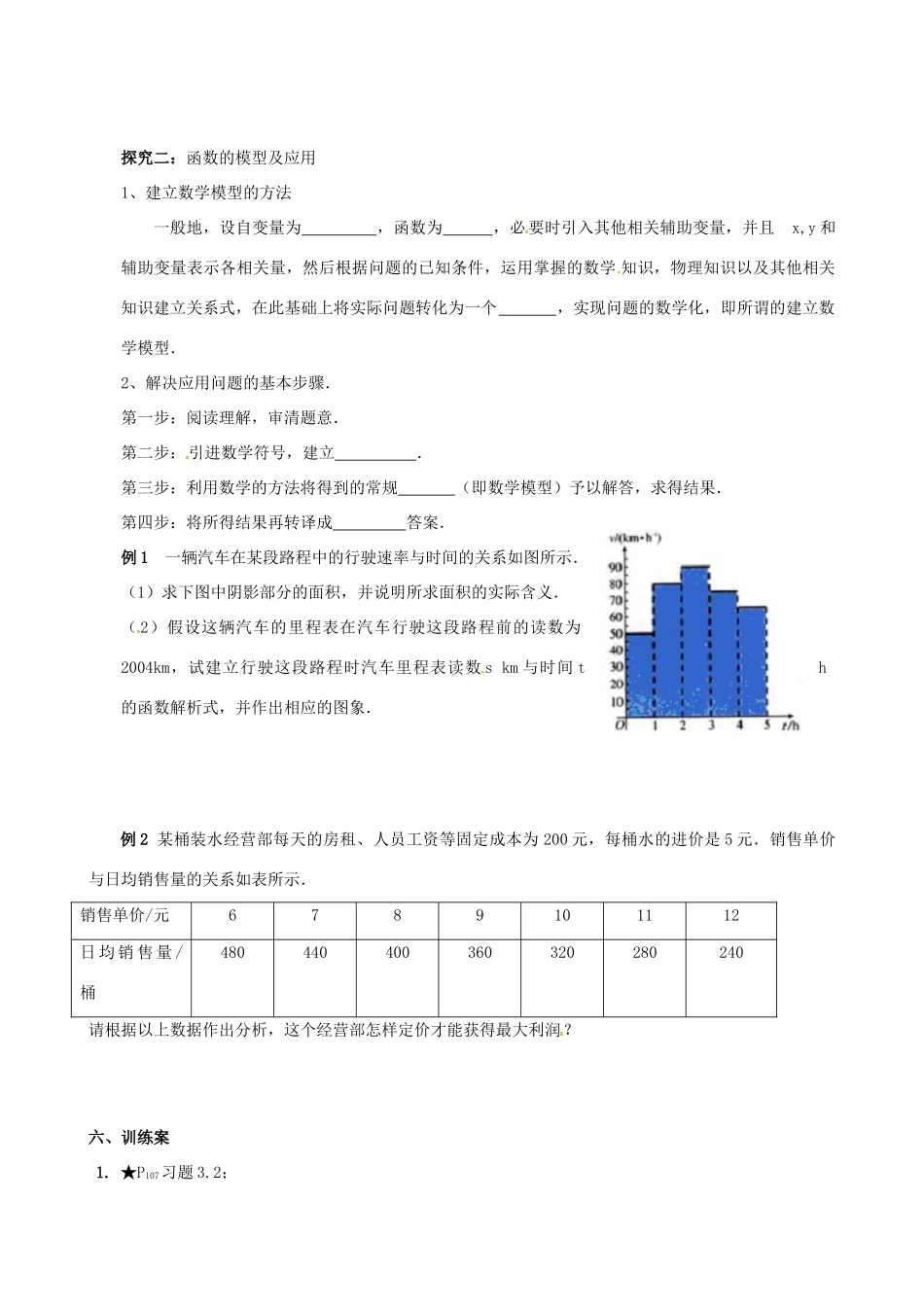
四川省古蔺县中学高中数学必修一 3.3.2 几类不同增长的函数模型(1)导学案一、教学目标:1. 结合实例体会直线上升、指数爆炸、对数增长等不同增长的函数 模型意义,理解它们的增长差异;2. 借助信息技术,利用函数图象及数据表格,比较指数函数、对数函数以及幂函数的增长差异;3. 能够通过题意,自建模型,解决实际的问题.二、教学重难点:1.教学重点:运用函数模型解决一些实际问题.2.教学难点:将实际问题转变 为数学模型.三、课时学法指导学生自学和教师引导相结合,通过实际问题的解决, 培养学生科学的提出问题、分析问题的能力.四、预习案: 完成任务情况自评: 学科组长评价: .1.任务布置:1:研读教材 P98 ——P106;2:思考解决应用题的一般程序?2.存在问题: 五、探究案探究一:幂、指、对函数的增长差异问题:幂函数、指数函数、对数函数在区间 上 的单调性如何?增长有差异吗?实验:函数,,,试计算: 12345678y1y2y3011.5822.322.582.813由表中的数据,你能得到什么结论?观察:在图像上分别标 出使不等式成立的自变量大的取值范围?说明增长差异?思考:由以上问题你能得出怎样的结论?探究二:函数的模型及应用1、建立数学模型的方法一般地,设自变量为 ,函数为 ,必要时引入其他相关辅助变量,并且 x,y 和辅助变量表示各相关量,然后根据问题的已知条件,运用掌握的数学 知识,物理知识以及其他相关知识建立关系式,在此基础上将实际问题转化为一个 ,实现问题的数学化,即所谓的建立数学模型.2、解决应用问题的基本步骤.第一步:阅读理解,审清题意.第二步:引进数学符号,建立 .第三步:利用数学的方法将得到的常规 (即数学模型)予以解答,求得结果.第四步:将所得结果再转译成 答案.例 1 一辆汽车在某段路程中的行驶速率与时间的关系如图所示.(1)求下图中阴影部分的面积,并说明所求面积的实际含义.( 2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004km,试建立行驶这段路程时汽车里程表读数 s km 与时间 t h的函数解析式,并作出相应的图象.例 2 某桶装水经营部每天的房租、人员工资等固定成本为 200 元,每桶水的进价是 5 元.销售单价与日均销售量的关系如表所示.销售单价/元6789101112日 均 销 售 量 /桶480440400360320280240请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?六、训练案1. ★P107习题 3.2; 2. ★★ 《聚焦课堂》3.3七、反思与小结: